ЬтФПФкШн
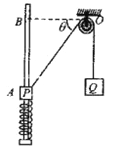
ЁОЬтФПЁПШчЭМЫљЪОЃЌГЄЮЊlжЪСПЮЊM=3kgЕФФОАхОВжЙЙтЛЌЫЎЦНЕиУцЩЯЃЌФОАхзѓЖЫЙЬЖЈвЛЧсЕЏЛЩЃЌЕЏЛЩгвЖЫСЌНгвЛИіЧсжЪБЁЦЌЃЌПЊЪМЪБЕЏЛЩДІгкздШЛГЄЖШЃЌБЁЦЌЮЛгкФОАхЕФжаЕуOЕуДІЃЌвЛжЪСПЮЊm=2kgЕФаЁЮяПщЃЈПЩвдЪгЮЊжЪЕуЃЉЃЌвдЫйЖШv0=4m/sГхЩЯФОАхЃЌХіЕНБЁЦЌКѓНЋЕЏЛЩбЙЫѕжСзюЖЬЃЌзюКѓЮяПщгжБЛЕЏЛиЕНOЕугвВрЃЌзюжеаЁЮяПщЛЌЕНРыФОАхгвЖЫЮЊ![]() ДІБуЫцФОАхвЛЦ№дЫЖЏЁЃФОАхЩЯБэУцOЕузѓВрЙтЛЌЃЌгвВрДжВкЃЌЮяПщгыOЕугвВржЎМфЕФЖЏФІВСвђЪ§ІЬ=0.3ЃЌжиСІМгЫйЖШg=10m/s2ЃЌзюДѓОВФІВССІЕШгкЛЌЖЏФІВССІЃЌЧѓЃК
ДІБуЫцФОАхвЛЦ№дЫЖЏЁЃФОАхЩЯБэУцOЕузѓВрЙтЛЌЃЌгвВрДжВкЃЌЮяПщгыOЕугвВржЎМфЕФЖЏФІВСвђЪ§ІЬ=0.3ЃЌжиСІМгЫйЖШg=10m/s2ЃЌзюДѓОВФІВССІЕШгкЛЌЖЏФІВССІЃЌЧѓЃК
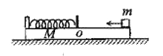
ЃЈ1ЃЉФОАхЕФГЄЖШlЃЛ
ЃЈ2ЃЉФОАхЕФзюДѓЫйЖШЃЛ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉ
ЃЈ2ЃЉ![]()
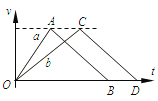
ЁОНтЮіЁПЃЈ1ЃЉЮяПщЁЂФОАхЁЂЕЏЛЩзщГЩЕФЯЕЭГЖЏСПЪиКуЃЌбЁЯђзѓЮЊе§ЃЌзюКѓЬхЯЕЫйЖШЮЊv
дђга:![]()
НтЕУ:v=1.6m/s
гЩФмСПЪиКуЖЈТЩЕУ:![]()
НтЕУ:![]()
ЃЈ2ЃЉЕБЮяПщдйДЮЛиЕНOЕуЪБЃЌФОАхЕФЫйЖШзюДѓЃЌЩшДЫЪБФОПщЫйЖШЮЊ![]() ЃЌФОАхЫйЖШЮЊ
ЃЌФОАхЫйЖШЮЊ![]() ЃЌгЩЖЏСПЪиКуЖЈТЩЕУ:
ЃЌгЩЖЏСПЪиКуЖЈТЩЕУ:![]()
гЩФмСПЪиКуЖЈТЩЕУ:![]()
СЊСЂНтЕУ:![]() ЃЈЩсШЅ0.8m/sЃЉ
ЃЈЩсШЅ0.8m/sЃЉ