Question

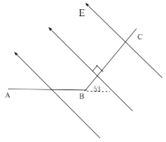
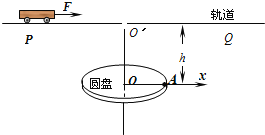
【题目】如图所示，半径R=0.4m的圆盘水平放置，绕竖直轴OO′匀速转动，在圆心O正上方=0.8m高处固定一水平轨道PQ，转轴和水平轨道交于O′点.一质量m=2kg的小车（可视为质点），在F=6N的水平恒力作用下（一段时间后，撤去该力），从O′左侧x0=2m处由静止开始沿轨道向右运动，当小车运动到O′点时，从小车上自由释放一小球，此时圆盘半径OA与轴重合。规定经过O点水平向右为轴正方向，小车与轨道间的动摩擦因数μ=0.2，g取10m/s2 ，求：

(1)为使小球刚好落在A点，圆盘转动的角速度应为多大？

(2)现在A点放一物体，其质量为1kg，通过一根最大拉力为（10π2-5）N的绳子与圆盘圆心O点连接，当圆盘角速度为(1)问中最小值时，为使绳子不拉断，问物体与圆盘的动摩擦因数μ′最小应为多大？

(3)为使小球能落到圆盘上，求水平拉力F作用的距离范围？

Answer 1

【答案】(1) (2)0.5 (3)

【解析】

(1)小球离开小车后，由于惯性将以离开小车时的速度作平抛运动

竖直反向有：

解得：

为使小球刚好落在A点则应满足：ωt=2kπ

解得：

(2)最小角速度为ω=5π

由牛顿第二定律:f+T=mRω2

当f、T分别取最大值时，有最小值,有：

得：

(3)①当球落到O点时，

得：

F撤去后，匀减速，a2=f/m=2.0m/s2

依题意得：x1+x2=2

联立得：x1=4/3m

②当球落到A点时，

先匀加速，后匀减速:

联立得x1=1.5m

故水平拉力F作用的距离范围：