题目内容
13. 如图是静电分选器的原理示意图,将磷酸盐和石英的混合颗粒由传送带送至两个竖直的带电平行板上方,颗粒经漏斗从电场区域中央处开始下落,经分选后的颗粒分别装入A、B桶中.混合颗粒离开漏斗进入电场时磷酸盐颗粒带正电,石英颗粒带负电,所有颗粒所带的电荷量与质量之比均为10-5C/kg.若已知两板间的距离为10cm,两板的竖直高度为50cm.设颗粒进入电场时的速度为零,颗粒间相互作用不计.如果要求两种颗粒离开两极板间的电场区域时恰好从两极板下边缘飞出.求(g=10m/s2)
如图是静电分选器的原理示意图,将磷酸盐和石英的混合颗粒由传送带送至两个竖直的带电平行板上方,颗粒经漏斗从电场区域中央处开始下落,经分选后的颗粒分别装入A、B桶中.混合颗粒离开漏斗进入电场时磷酸盐颗粒带正电,石英颗粒带负电,所有颗粒所带的电荷量与质量之比均为10-5C/kg.若已知两板间的距离为10cm,两板的竖直高度为50cm.设颗粒进入电场时的速度为零,颗粒间相互作用不计.如果要求两种颗粒离开两极板间的电场区域时恰好从两极板下边缘飞出.求(g=10m/s2)(1)两极板间所加的电压应多大?
(2)若带电平行板的下端距A、B桶底的高度H=1.3m,求颗粒落至桶底时速度的大小.(本问计算结果保留整数)
分析 (1)根据受力情况可知颗粒进入电场后在竖直方向做自由落体运动,而在水平方向做匀加速直线运动.
(2)颗粒从离开漏斗到到达传送带受重力和电场力,电场力做功与路径无关,只与初末位置的电势差有关,故电场力所做的功为q$\frac{U}{2}$,重力做功也与路径无关只与初末位置的高度差有关,故重力所做的功为mg(l+H),根据动能定理即可求出落至传送带时的速度大小
解答 解:(1)由于a颗粒带正电,故电场方向向左,所以左板带负电荷,右板带正电荷
依题意,颗粒在平行板的竖直方向上做自由落体运动,故满足L=$\frac{1}{2}$gt2 ①
在水平方向上做匀加速直线运动,加速度大小为a=$\frac{qU}{md}$②
离开电场时颗粒在水平方向的位移为$\frac{d}{2}$
由匀变速直线运动规律得:$\frac{d}{2}=\frac{1}{2}$at2 ③
联立①②③得:U=$\frac{m{d}^{2}g}{2qL}$=1×104V
(2)在颗粒下落的整个过程中,根据动能定理得:
$\frac{1}{2}$qU+mg(L+H)=$\frac{1}{2}$mv2
代入数据得:v=6 m/s?
答:(1)两极板间所加的电压应为1×104V
(2)若带电平行板的下端距A、B桶底高度为H=1.3m,求颗粒落至桶底时速度的大小为6m/s
点评 本题属于带电粒子在电场中的偏转问题,结合平抛运动的规律与动能定理求解,属于中档题偏难一些.

练习册系列答案
相关题目
4. 如图所示,斜面AE被分成四个相等的部分,一物体由A点从静止释放匀加速直线下滑,下列结论正确的是( )
如图所示,斜面AE被分成四个相等的部分,一物体由A点从静止释放匀加速直线下滑,下列结论正确的是( )
 如图所示,斜面AE被分成四个相等的部分,一物体由A点从静止释放匀加速直线下滑,下列结论正确的是( )
如图所示,斜面AE被分成四个相等的部分,一物体由A点从静止释放匀加速直线下滑,下列结论正确的是( )| A. | 物体到达各点的速度之比为vB:vC:vD:vE=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| B. | 物体到达各点所经历的时间之比tE=2tB=$\sqrt{2}$tC=$\frac{2}{\sqrt{3}}$tD | |
| C. | 物体通过每一部分时,其速度的增量均相等 | |
| D. | 物体从A到E的平均速度等于物体过B点的瞬时速度 |
8.电源的电动势和内阻都保持一定,在外电路的电阻逐渐减小的过程中,下面说法中正确的是( )
| A. | 电源的输出功率一定逐渐变小 | B. | 电源内部消耗的功率一定逐渐变大 | ||
| C. | 电源的效率一定逐渐变小 | D. | 电源的总功率一定逐渐变大 |
18.如图1所示某同学探究弹力与弹簧伸长量的关系
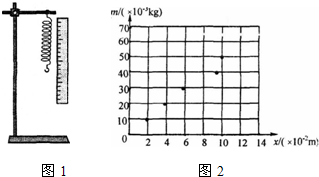
①将弹簧悬挂在铁架台上,将最小刻度为毫米的刻度尺固定在弹簧一侧,弹簧轴线和刻度尺都应在竖直方向(填“水平”或“竖直”)
②弹簧自然悬挂,待弹簧稳定时,长度记为L0,弹簧下端挂上砝码盘时,长度记为Lx;在砝码盘中每次增加10g砝码,弹簧长度依次记为L1至L6,数据如表:
表中有一个数值记录不规范,代表符号为L3
③该同学在坐标纸上取砝码的质量为纵轴,弹簧长度与Lx的差值为横轴,如图是他根据表中数据已经描好的前5个点,请描出第6个点并完成该图象
④由图可知弹簧的劲度系数为4.9N/m;通过图和表可知砝码盘的质量为10g(结果保留两位有效数字,重力加速度取9.8m/s2)

①将弹簧悬挂在铁架台上,将最小刻度为毫米的刻度尺固定在弹簧一侧,弹簧轴线和刻度尺都应在竖直方向(填“水平”或“竖直”)
②弹簧自然悬挂,待弹簧稳定时,长度记为L0,弹簧下端挂上砝码盘时,长度记为Lx;在砝码盘中每次增加10g砝码,弹簧长度依次记为L1至L6,数据如表:
| 代表符号 | L0 | Lx | L1 | L2 | L3 | L4 | L5 | L6 |
| 数值(cm) | 25.35 | 27.35 | 29.35 | 31.30 | 33.4 | 37.15 | 37.45 | 39.30 |
③该同学在坐标纸上取砝码的质量为纵轴,弹簧长度与Lx的差值为横轴,如图是他根据表中数据已经描好的前5个点,请描出第6个点并完成该图象
④由图可知弹簧的劲度系数为4.9N/m;通过图和表可知砝码盘的质量为10g(结果保留两位有效数字,重力加速度取9.8m/s2)
5. 如图所示的电路,A、B、C为三个相同的灯泡,其电阻大于电源内阻,当变阻器的滑动触头P向上移动时( )
如图所示的电路,A、B、C为三个相同的灯泡,其电阻大于电源内阻,当变阻器的滑动触头P向上移动时( )
 如图所示的电路,A、B、C为三个相同的灯泡,其电阻大于电源内阻,当变阻器的滑动触头P向上移动时( )
如图所示的电路,A、B、C为三个相同的灯泡,其电阻大于电源内阻,当变阻器的滑动触头P向上移动时( )| A. | A灯和B灯和C灯都变暗 | |
| B. | A灯变亮,B灯变暗,C灯变亮 | |
| C. | 电源释放的总电功率减小,电源的供电效率升高 | |
| D. | 电源输出的电功率增大,电源的供电效率降低 |
2.2004年10月19日,中国第一颗业务型同步气象卫星--“风云二号C”发射升空,并进入预定轨道.下列关于这颗卫星在轨道上运行的描述,正确的有( )
| A. | 速度大于7.9km/s | B. | 周期等于地球自转周期 | ||
| C. | 向心加速度小于地面重力加速度 | D. | 位于赤道正上空 |
3.由下列哪些现象可以说明光是横波( )
| A. | 光的偏振现象 | B. | 光的色散现象 | ||
| C. | 光的全反射现象 | D. | 光的干涉和衍射现象 |
 某同学在“用多用电表探索黑箱内的电学元件”时,在图中A、B、C三点,
某同学在“用多用电表探索黑箱内的电学元件”时,在图中A、B、C三点,