题目内容
1.一辆质量2t的小轿车,驶过半径R=50m的一段圆弧形桥面,重力加速度g=10m/s2.求:(1)若桥面为凹形,汽车以20m/s的速度通过桥面最低点时,对桥面压力是多大?
(2)若桥面为凸形,汽车以10m/s的速度通过桥面最高点时,对桥面压力是多大?
(3)汽车以多大速度通过凸形桥面顶点时,对桥面刚好没有压力?
分析 轿车在凹形桥和凸形桥的最低点和最高点,靠重力和支持力的合力提供向心力,根据牛顿第二定律求出桥面对轿车的支持力,从而得出轿车对桥面的压力.当轿车对凸形桥的压力为零时,靠重力提供向心力,根据牛顿第二定律求出汽车的速度.
解答 解:(1)过凹形桥时,由牛顿第二定律有:
${N}_{1}-mg=m\frac{{v}^{2}}{R}$
解得:N1=3.6×104N
由牛顿第三定律得,车对桥的压力大小为3.6×104N
(2)过凸形桥时,由牛顿第二定律有:
${mg-N}_{2}=m\frac{{v}^{2}}{R}$
解得:N2=1.6×104N
由牛顿第三定律得,车对桥的压力大小为1.6×104N
(3)当对桥面刚好无压力时,只受重力.
$mg=m\frac{{v}^{2}}{R}$
解得:v=$\sqrt{gR}=10\sqrt{5}m/s$
答:(1)若桥面为凹形,汽车以20m/s的速度通过桥面最低点时,对桥面压力是3.6×104N;
(2)若桥面为凸形,汽车以10m/s的速度通过桥面最高点时,对桥面压力是1.6×104N;
(3)汽车以$10\sqrt{5}m/s$的速度通过凸形桥面顶点时,对桥面刚好没有压力.
点评 解决本题的关键搞清向心力的来源,根据牛顿第二定律进行求解,知道当轿车对凸形桥的压力为零时,靠重力提供向心,难度不大,属于基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
11.不计空气的作用,小球沿固定光滑斜面下滑的过程中受到的作用力共有( )


| A. | 一个 | B. | 两个 | C. | 三个 | D. | 四个 |
12.关于速度和加速度的关系,下列说法正确的是( )
| A. | 加速度很大,说明速度一定很大 | |
| B. | 加速度很大,说明速度的变化一定很大 | |
| C. | 加速度很大,说明速度的变化率一定很大 | |
| D. | 加速度很大,速度有可能很小 |
9.如图是某一物体的运动图象,下列说法正确的是( )


| A. | 物体存前2s内的位移为20m | B. | 物体在6s末回到2s末时的位置 | ||
| C. | 物体在5s末回到出发点 | D. | 物体在前6s内的位移为30m |
16.如图所示,物块质量为m,一直随转筒一起以角速度ω绕竖直轴做匀速圆周运动,以下描述正确的是( )
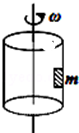

| A. | 物块所需向心力由圆筒对物块的摩擦力提供 | |
| B. | 物体受重力、摩擦力、向心力作用 | |
| C. | 若角速度ω增大,物块所受摩擦力增大 | |
| D. | 若角速度ω增大,物块所受弹力增大 |
6. 一个带电粒子(重力可忽略不计),沿垂直于磁场的方向射入一匀强磁场,粒子的一段径迹如图所示.径迹上的每一小段都可近似看成圆弧.由于带电粒子使沿途的空气电离,粒子的动能逐渐减小(带电量不变)从图中情况可以确定( )
一个带电粒子(重力可忽略不计),沿垂直于磁场的方向射入一匀强磁场,粒子的一段径迹如图所示.径迹上的每一小段都可近似看成圆弧.由于带电粒子使沿途的空气电离,粒子的动能逐渐减小(带电量不变)从图中情况可以确定( )
 一个带电粒子(重力可忽略不计),沿垂直于磁场的方向射入一匀强磁场,粒子的一段径迹如图所示.径迹上的每一小段都可近似看成圆弧.由于带电粒子使沿途的空气电离,粒子的动能逐渐减小(带电量不变)从图中情况可以确定( )
一个带电粒子(重力可忽略不计),沿垂直于磁场的方向射入一匀强磁场,粒子的一段径迹如图所示.径迹上的每一小段都可近似看成圆弧.由于带电粒子使沿途的空气电离,粒子的动能逐渐减小(带电量不变)从图中情况可以确定( )| A. | 粒子从a到b,带正电 | B. | 粒子从a到b,带负电 | ||
| C. | 粒子从b到a,带正电 | D. | 粒子从b到a,带负电 |
10.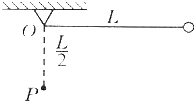 小金属球质量为m、用长L的轻悬线固定于O点,在O点的正下方$\frac{L}{2}$处钉有一颗钉子P,把悬线沿水平方向拉直,如图所示,无初速度释放,当悬线碰到钉子后的瞬时(设线没有断),则( )
小金属球质量为m、用长L的轻悬线固定于O点,在O点的正下方$\frac{L}{2}$处钉有一颗钉子P,把悬线沿水平方向拉直,如图所示,无初速度释放,当悬线碰到钉子后的瞬时(设线没有断),则( )
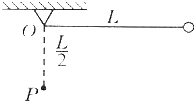 小金属球质量为m、用长L的轻悬线固定于O点,在O点的正下方$\frac{L}{2}$处钉有一颗钉子P,把悬线沿水平方向拉直,如图所示,无初速度释放,当悬线碰到钉子后的瞬时(设线没有断),则( )
小金属球质量为m、用长L的轻悬线固定于O点,在O点的正下方$\frac{L}{2}$处钉有一颗钉子P,把悬线沿水平方向拉直,如图所示,无初速度释放,当悬线碰到钉子后的瞬时(设线没有断),则( )| A. | 小球的线速度突然减小到零 | B. | 悬线的张力突然增大 | ||
| C. | 小球的角速度不变 | D. | 小球的向心加速度不变 |
11.有一个电子器件,当其两端电压高于100V时导电,等于或低于100V时则不导电,若把这个电子器件接到100V、50Hz的正弦交流电源上,这个电子器件将( )
| A. | 不导电 | B. | 每秒钟导电50次 | ||
| C. | 每秒钟内导电100次 | D. | 每次导电的时间为0.005 s |
 如图是静电分选器的原理示意图,将磷酸盐和石英的混合颗粒由传送带送至两个竖直的带电平行板上方,颗粒经漏斗从电场区域中央处开始下落,经分选后的颗粒分别装入A、B桶中.混合颗粒离开漏斗进入电场时磷酸盐颗粒带正电,石英颗粒带负电,所有颗粒所带的电荷量与质量之比均为10-5C/kg.若已知两板间的距离为10cm,两板的竖直高度为50cm.设颗粒进入电场时的速度为零,颗粒间相互作用不计.如果要求两种颗粒离开两极板间的电场区域时恰好从两极板下边缘飞出.求(g=10m/s2)
如图是静电分选器的原理示意图,将磷酸盐和石英的混合颗粒由传送带送至两个竖直的带电平行板上方,颗粒经漏斗从电场区域中央处开始下落,经分选后的颗粒分别装入A、B桶中.混合颗粒离开漏斗进入电场时磷酸盐颗粒带正电,石英颗粒带负电,所有颗粒所带的电荷量与质量之比均为10-5C/kg.若已知两板间的距离为10cm,两板的竖直高度为50cm.设颗粒进入电场时的速度为零,颗粒间相互作用不计.如果要求两种颗粒离开两极板间的电场区域时恰好从两极板下边缘飞出.求(g=10m/s2)