题目内容
 如图所示,两平行金属导轨间距l=0.5m,导轨与水平面成θ=37°.导轨上端连接有E=6V、r=1Ω的电源和滑动变阻器.长度也为l的金属棒ab垂直导轨放置且与导轨接触良好,金属棒的质量m=0.2kg、电阻R0=1Ω,整个装置处在竖直向上的匀强磁场中,金属棒一直静止在导轨上.当滑动变阻器的阻值R=1Ω时金属棒刚好与导轨间无摩擦力.g取10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,两平行金属导轨间距l=0.5m,导轨与水平面成θ=37°.导轨上端连接有E=6V、r=1Ω的电源和滑动变阻器.长度也为l的金属棒ab垂直导轨放置且与导轨接触良好,金属棒的质量m=0.2kg、电阻R0=1Ω,整个装置处在竖直向上的匀强磁场中,金属棒一直静止在导轨上.当滑动变阻器的阻值R=1Ω时金属棒刚好与导轨间无摩擦力.g取10m/s2,sin37°=0.6,cos37°=0.8.求:(1)此时电路中的电流I;
(2)当滑动变阻器接入电路的电阻为4Ω时金属棒受到的摩擦力.
分析:(1)根据闭合电路欧姆定律求解此时电路中的电流I;
(2)根据题意,滑动变阻器的阻值R=1Ω时金属棒刚好与导轨间无摩擦力,分析棒的受力,根据平衡条件和安培力可求出磁感应强度B.再运用闭合电路欧姆定律求出滑动变阻器接入电路的电阻为4Ω时电路中电流,求出棒所受的安培力,判断摩擦力的方向,再根据平衡条件求解摩擦力.
(2)根据题意,滑动变阻器的阻值R=1Ω时金属棒刚好与导轨间无摩擦力,分析棒的受力,根据平衡条件和安培力可求出磁感应强度B.再运用闭合电路欧姆定律求出滑动变阻器接入电路的电阻为4Ω时电路中电流,求出棒所受的安培力,判断摩擦力的方向,再根据平衡条件求解摩擦力.
解答: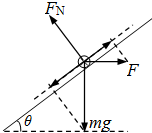 解:(1)根据闭合电路欧姆定律,当滑动变阻器的电阻为R1=1Ω时,
解:(1)根据闭合电路欧姆定律,当滑动变阻器的电阻为R1=1Ω时,
电流 I1=
=
=2A
(2)金属棒受重力mg、安培力F和支持力FN如图.
根据平衡条件可得,mgsinθ=F1cosθ
又 F1=BI1l
联立上式,解得磁感应强度 B=
=
=1.5T
当滑动变阻器的电阻为R2=4Ω时,电流 I2=
=
A=1A
又 F2=BI2l=1.5×1×0.5N=0.75N
mgsinθ=0.2×10×sin37°=1.2N
∴mgsinθ>F2cosθ,故金属棒受到沿导轨平面向上的摩擦力Ff
根据平衡条件可得,mgsinθ=F2cosθ+Ff
联立解得:Ff=mgsinθ-F2cosθ=0.2×10×sin37°-0.75×cos37°=0.6N
答:(1)此时电路中的电流I为2A;(2)当滑动变阻器接入电路的电阻为4Ω时金属棒受到的摩擦力为0.6N.
 解:(1)根据闭合电路欧姆定律,当滑动变阻器的电阻为R1=1Ω时,
解:(1)根据闭合电路欧姆定律,当滑动变阻器的电阻为R1=1Ω时,电流 I1=
| E |
| R1+R0+r |
| 6 |
| 1+1+1 |
(2)金属棒受重力mg、安培力F和支持力FN如图.
根据平衡条件可得,mgsinθ=F1cosθ
又 F1=BI1l
联立上式,解得磁感应强度 B=
| mgtanθ |
| I1l |
| 0.2×10×tan37° |
| 2×0.5 |
当滑动变阻器的电阻为R2=4Ω时,电流 I2=
| E |
| R2+R0+r |
| 6 |
| 4+1+1 |
又 F2=BI2l=1.5×1×0.5N=0.75N
mgsinθ=0.2×10×sin37°=1.2N
∴mgsinθ>F2cosθ,故金属棒受到沿导轨平面向上的摩擦力Ff
根据平衡条件可得,mgsinθ=F2cosθ+Ff
联立解得:Ff=mgsinθ-F2cosθ=0.2×10×sin37°-0.75×cos37°=0.6N
答:(1)此时电路中的电流I为2A;(2)当滑动变阻器接入电路的电阻为4Ω时金属棒受到的摩擦力为0.6N.
点评:本题是通电导体在磁场中平衡问题,运用闭合电路欧姆定律和平衡条件求B是关键,再根据平衡条件求解摩擦力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
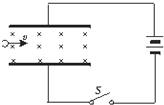 如图所示,两平行金属板水平放置,开始开关S合上使平行板电容器带电.板间存在垂直纸面向里的匀强磁场.一个不计重力的带电粒子恰能以水平向右的速度沿直线通过两板.在以下方法中,能使带电粒子仍沿水平直线通过两板的是( )
如图所示,两平行金属板水平放置,开始开关S合上使平行板电容器带电.板间存在垂直纸面向里的匀强磁场.一个不计重力的带电粒子恰能以水平向右的速度沿直线通过两板.在以下方法中,能使带电粒子仍沿水平直线通过两板的是( )| A、把两板间距离减小一半,同时把粒子速率增加一倍 | B、把两板的距离增大一倍,同时把板间的磁感应强度增大一倍 | C、把开关S断开,两板的距离增大一倍,同时把板间的磁感应强度减为一半 | D、把开关S断开,两板的距离减小一半,同时把粒子速率减小一半 |
 如图所示,两平行金属板间有一匀强电场,板长为L,板间距离为d,在 板右端L处有一竖直放置的光屏M,一带电荷量为q,质量为m的质点从两板中央射入板间,最后垂直打在M屏上,则下列结论正确的是( )
如图所示,两平行金属板间有一匀强电场,板长为L,板间距离为d,在 板右端L处有一竖直放置的光屏M,一带电荷量为q,质量为m的质点从两板中央射入板间,最后垂直打在M屏上,则下列结论正确的是( )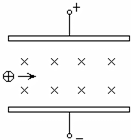 如图所示,两平行金属板中有相互垂直的匀强电场和匀强磁场,带正电的粒子(不计粒子的重力)从两板中央垂直电场、磁场入射.它在金属板间运动的轨迹为水平直线,如图中虚线所示.若使粒子飞越金属板间的过程中向上板偏移,则可以采取下列的正确措施为( )
如图所示,两平行金属板中有相互垂直的匀强电场和匀强磁场,带正电的粒子(不计粒子的重力)从两板中央垂直电场、磁场入射.它在金属板间运动的轨迹为水平直线,如图中虚线所示.若使粒子飞越金属板间的过程中向上板偏移,则可以采取下列的正确措施为( ) 如图所示,两平行金属板的间距等于极板的长度,现有重力不计的正离子束以相同的初速度v0平行于两板从两板正中间射入.第一次在两极板间加恒定电压,建立场强为E的匀强电场,则正离子束刚好从上极板边缘飞出.第二次撤去电场,在两板间建立磁感应强度为B、方向垂直于纸面的匀强磁场,正离子束刚好从下极板边缘飞出,则E和B的大小之比为( )
如图所示,两平行金属板的间距等于极板的长度,现有重力不计的正离子束以相同的初速度v0平行于两板从两板正中间射入.第一次在两极板间加恒定电压,建立场强为E的匀强电场,则正离子束刚好从上极板边缘飞出.第二次撤去电场,在两板间建立磁感应强度为B、方向垂直于纸面的匀强磁场,正离子束刚好从下极板边缘飞出,则E和B的大小之比为( ) 如图所示,两平行金属板间电场是匀强电场,场强大小为1.0×104V/m,A、B两板相距1cm,C点与A相距0.4cm,若B接地,则A、C间电势差UAC=
如图所示,两平行金属板间电场是匀强电场,场强大小为1.0×104V/m,A、B两板相距1cm,C点与A相距0.4cm,若B接地,则A、C间电势差UAC=