题目内容
20.平直的公路上,一辆汽车以加速度a从静止开始启动,人在车后面,以初速度v0追赶汽车,开始时,人与车之间的距离为s0,设人与车速度相等前,人比车多走的距离为△s,判断人是否能追上车?(1)当△s>s0时,追上了,需要求何时追上?
(2)当△s<s0时,追不上,需要求人与车之间的最小距离smin?
(3)当△s=s0时,恰好追上,则人匀速运动的速度至少为多少?
分析 (1)当△s>s0时,人会追上汽车,结合位移关系,运用运动学公式求出追及的时间.
(2)当△s<s0时,人不会追上汽车,当速度相等时,两者之间有最小距离,结合速度时间公式和位移公式求出最小距离.
(3)当△s=s0时,恰好追上,根据位移关系,抓住速度相等时恰好追上求出人匀速运动的最小速度.
解答 解:(1)在速度相等前,人的速度大于车的速度,若△s>s0时,人会追上汽车.
根据${v}_{0}t={s}_{0}+\frac{1}{2}a{t}^{2}$解得:t=$\frac{{v}_{0}-\sqrt{{{v}_{0}}^{2}-2a{s}_{0}}}{a}$.
(2)若△s<s0时,追不上,速度相等时有最小距离.速度相等经历的时间为:$t=\frac{{v}_{0}}{a}$,
$△x={v}_{0}\frac{{v}_{0}}{a}-\frac{{{v}_{0}}^{2}}{2a}=\frac{{{v}_{0}}^{2}}{2a}$.
则最小距离smin=s0-△x=${s}_{0}-\frac{{{v}_{0}}^{2}}{2a}$.
(3)当△s=s0时,恰好追上,根据${v}_{0}\frac{{v}_{0}}{a}=\frac{{{v}_{0}}^{2}}{2a}+{s}_{0}$,解得最小初速度为:${v}_{0}=\sqrt{2a{s}_{0}}$.
答:(1)当△s>s0时,追上了,需要经历$\frac{{v}_{0}-\sqrt{{{v}_{0}}^{2}-2a{s}_{0}}}{a}$的时间追上;
(2)当△s<s0时,追不上,人与车之间的最小距离为${s}_{0}-\frac{{{v}_{0}}^{2}}{2a}$;
(3)当△s=s0时,恰好追上,则人匀速运动的速度至少为$\sqrt{2a{s}_{0}}$.
点评 本题考查了运动学中的追及问题,抓住临界状态,结合位移关系,运动学公式灵活求解,难度中等.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 如图所示,质量为M的A物体和质量为m的B物体叠放在竖直弹簧上并保持静止(m=2M),现用大小为mg的恒力F竖直向上拉物体B,竖直向上运动的距离为h时B与A分离,则下列说法正确的是( )
如图所示,质量为M的A物体和质量为m的B物体叠放在竖直弹簧上并保持静止(m=2M),现用大小为mg的恒力F竖直向上拉物体B,竖直向上运动的距离为h时B与A分离,则下列说法正确的是( )| A. | B和A刚分离时,弹簧为原长 | |
| B. | B和A刚分离时,弹簧处于压缩状态 | |
| C. | 弹簧的劲度系数为$\frac{mg}{h}$ | |
| D. | 在B与A分离之前,它们做匀加速直线运动 |
 一理想变压器原、副线圈的匝数比为10:1,原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器的触头.下列说法正确的是( )
一理想变压器原、副线圈的匝数比为10:1,原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器的触头.下列说法正确的是( )| A. | 副线圈输出电压的频率为50Hz | |
| B. | 副线圈输出电压的有效值为31 V | |
| C. | 原线圈中输入电压的有效值为310V | |
| D. | P向右移动时,变压器的输出功率不变 |
 如图所示,平行板电容器与电动势为E的直流电源(内阻不计)连接,下极板接地.一带电油滴位于容器中的P点且恰好处于平衡状态.现将平行板电容器的上极板不动,下极板竖直向下移动一小段距离,则说法正确的是( )
如图所示,平行板电容器与电动势为E的直流电源(内阻不计)连接,下极板接地.一带电油滴位于容器中的P点且恰好处于平衡状态.现将平行板电容器的上极板不动,下极板竖直向下移动一小段距离,则说法正确的是( )| A. | 带电油滴将沿竖直方向向上运动 | |
| B. | P点的电势将升高 | |
| C. | 移动下板的过程中带电油滴的机械能将增加 | |
| D. | 电容器的电容减小,极板带电量将增大 |
| A. | 加速度与速度无必然联系 | B. | 速度减小时,加速度也一定减小 | ||
| C. | 速度为零,加速度也一定为零 | D. | 速度增大时,加速度不一定增大 |
 如图所示为小型旋转电枢式交流发电机,电阻r=lΩ的矩形线圈在磁感应强度为B的匀强磁场中,绕垂直于磁场方向的固定轴OO′匀速转动,线圈的两端经集流环和电刷与电路连接,滑动变阻器R的最大阻值为6Ω,滑动片P位于滑动变阻器距下端$\frac{1}{3}$处,定值电阻R1=2Ω,其他电阻不计,线圈匀速转动的周期T=0.02s.闭合开关S,从线圈平面与磁场方向平行时开始计时,线圈转动过程中理想电压表示数是5V.下列说法正确的是( )
如图所示为小型旋转电枢式交流发电机,电阻r=lΩ的矩形线圈在磁感应强度为B的匀强磁场中,绕垂直于磁场方向的固定轴OO′匀速转动,线圈的两端经集流环和电刷与电路连接,滑动变阻器R的最大阻值为6Ω,滑动片P位于滑动变阻器距下端$\frac{1}{3}$处,定值电阻R1=2Ω,其他电阻不计,线圈匀速转动的周期T=0.02s.闭合开关S,从线圈平面与磁场方向平行时开始计时,线圈转动过程中理想电压表示数是5V.下列说法正确的是( )| A. | 电阻R1消耗的功率为$\frac{2}{3}$W | |
| B. | 0.02 s时滑动变阻器R两端的电压瞬时值为零 | |
| C. | 线圈产生的电动势e随时间t变化的规律是e=6$\sqrt{2}$sin100πt(V) | |
| D. | 线圈从开始计时到$\frac{1}{200}$s的过程中,通过R1的电荷量为$\frac{{\sqrt{2}}}{200π}$C |
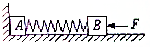 如图所示,质量分别为m和2m的A、B两个木块间用轻弹簧相连,放在光滑水平面上,A靠近竖直墙,用水平力F将B向左压,静止后弹簧储存的弹性势能为E,若突然撤去F,那么A离开墙后,弹簧的弹性势能最大值将是多大?
如图所示,质量分别为m和2m的A、B两个木块间用轻弹簧相连,放在光滑水平面上,A靠近竖直墙,用水平力F将B向左压,静止后弹簧储存的弹性势能为E,若突然撤去F,那么A离开墙后,弹簧的弹性势能最大值将是多大?