题目内容
【题目】某电视台正在策划的“快乐向前冲”节目的场地设施如图所示，AB为水平直轨道，上面安装有电动悬挂器，可以载人运动，下方水面上漂浮着一个半径为R铺有海绵垫的转盘，转盘轴心离平台的水平距离为L，平台边缘与转盘平面的高度差H。选手抓住悬挂器后，按动开关，在电动机的带动下从A点沿轨道做初速为零、加速度为a的匀加速直线运动。起动后2 s悬挂器脱落。设人的质量为m（看作质点），人与转盘间的最大静摩擦力为μmg，重力加速度为g.
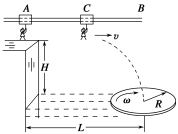
（1）假设选手落到转盘上瞬间相对转盘速度立即变为零，为保证他落在任何位置都不会被甩下转盘，转盘的角速度ω应限制在什么范围？
（2）已知H＝3.2 m，R =0.9 m，取g＝10 m/s2，当a＝2 m/s2时选手恰好落到转盘的圆心上，求L = ?
（3）选手要想成功落在转盘上，可以选择的加速度范围？
【答案】（1）
（2）7.2 m（3）a1 = 1.75 m/s2或者a2 = 2.25 m/s2
【解析】
试题分析：(1)设人落在圆盘边缘处不至被甩下，临界情况下，最大静摩擦力提供向心力
则有：μmg = mω2R （2分）
解得
取≤ （2分）
(2)匀加速过程
m = 4 m vc = at = 4 m/s （2分）
平抛过程
得t2 = 0.8 s （1分）
x2 = vc t2 = 4×0.8 m = 3.2 m （1分）
故 L = x1 + x2 = 7.2 m （2分）
(3)分析知a最小时落在转盘左端，a最大时落在转盘右端
据
解得a1 = 1.75 m/s2 （2分）
据
解得a2 = 2.25 m/s2 （2分）
练习册系列答案
相关题目
