题目内容
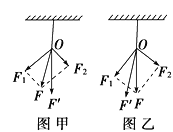
【题目】如图所示，轻质弹簧的上端固定在电梯的天花板上，弹簧下端悬挂一个小球，电梯中有质量为50kg的乘客，在电梯运行时乘客发现轻质弹簧的伸长量始终是电梯静止时的四分之三，已知重力加速度g=10m/s2，由此可判断（ ）
A. 电梯可能加速下降，加速度大小为5m/s2
B. 电梯可能减速上升，加速度大小为2.5m/s2
C. 乘客处于失重状态
D. 乘客对电梯地板的压力为425 N
【答案】BC
【解析】电梯静止不动时，小球受力平衡，有mg=kx，电梯运行时弹簧的伸长量变为静止时的3/4，说明弹力变小了，根据牛顿第二定律，有mg-
kx=ma，即a=2.5 m/s2，加速度向下，电梯可能加速下降或减速上升，乘客处于失重状态，选项AC错误，选项B正确；以乘客为研究对象，根据牛顿第二定律可得：m′g-FN=m′a，乘客对地板的压力大小为FN=m′g-m′a=500 -50×2.5 N=375 N，选项D错误．故选B．
【题目】某同学在“研究匀变速直线运动”的实验中，用打点计时器记录了被小车拖动的纸带的运动情况，在纸带上确定出A、B、C、D、E、F、G共7个计数点，其相邻点间的距离如图所示，每两个相邻的计数点之间的时间间隔为0.10 s。
(1)试根据纸带上各个计数点间的距离，计算打下B、C、D、E、F五个点时小车的瞬时速度，并将各个速度值填在下面的横线上。(保留到小数点后两位)
计数点序号 | B | C | D | E | F |
计数点对应的时刻/s | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
通过计数点时小车 的速度 | ____ | 0.48 | ____ | 0.64 | 0.72 |
(2)以A点为计时零点，将B、C、D、E、F各个时刻的瞬时速度标在如图所示的坐标纸上，并画出小车的瞬时速度随时间变化的关系图线________。
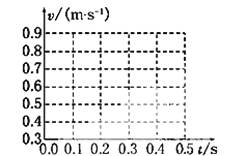
(3)根据第(2)问中画出的v－t图线，求出小车运动的加速度为________ m/s2。(保留到小数点后两位)
