Question

【题目】如图所示，轻质弹簧的一端固定在墙上，另一端与质量为2m的物体A相连，A放在光滑水平面上，有一质量为m的物体B，从高h处由静止开始沿光滑曲面滑下，与A相碰（时间极短）后一起将弹簧压缩，弹簧复原过程中某时刻B与A分开且沿曲面返回上升．下列说法正确的是（ ）

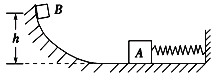
A.物体B、A组成的系统，在发生碰撞的过程中动量守恒，在弹簧被压缩的过程中机械能守恒

B.物体A对B做了负功

C.物体B返回过程中能达到的最大高度为h

D.物体A对B的冲量大小为

Answer 1

【答案】BD

【解析】

A．物体B、A组成的系统，在发生碰撞的过程中合力为零，动量守恒。在弹簧被压缩的过程中，弹簧对A做负功，则系统的机械能减少，故A错误。

B．对B下滑过程，据机械能守恒定律可得：

则B刚到达水平地面的速度

．

A、B碰撞过程，以AB组成的系统为研究对象，取向右为正方向，根据动量守恒定律可得：

mv0=3mv

得A与B碰撞后的共同速度为

对B，根据动能定理得：物体A对B做的功

故B正确。

C．当弹簧再次恢复原长时，A与B将分开，B以v的速度沿斜面上滑，根据机械能守恒定律可得

B能达到的最大高度为，故C错误。

D．对B，取水平向左为正方向，由动量定理得：物体A对B的冲量

故D正确。