��Ŀ����
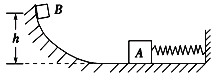
����Ŀ����ͼ��ʾ�������뾶��ΪR���ķ�֮Բ�����ɵĹ⻬ϸ�ܵ�ABC��ֱ���ã��ҹ̶��ڹ⻬ˮƽ���ϣ�Բ������O1O2ˮƽ���ᵯ����˹̶�����ֱ���ϣ��Ҷ�������Ϊm��С��Ӵ�����˨�ӣ�С���ֱ����С�ڹܵ��ھ�����������ΪR�ĺ��ӹ̶���ˮƽ���ϣ��������DG���ܵ��Ҷ�C��ˮƽ����ΪR����ʼʱ���ɴ�������״̬�����еĵ�������Ϊ6mgR������gΪ�������ٶȣ����������С���뿪���ɽ���ܵ�������C���׳��������ABC��ľ�н���EFGD��ͬһ��ֱ���ڣ�
(1)��С��C��ʱ�Ķ��ܣ�
(2)��С��C��ʱ�Թ����ѹ����
(3)С���C���׳�����ֱ�ӻ��к��ӵײ�ʱ�����۵�������ʱ������������ʲô����?

���𰸡�(1)![]() ��(2)
��(2)![]() ��������ֱ���ϣ�(3)
��������ֱ���ϣ�(3) ![]()
��������
(1)�������������С���˶���![]() ����̣����ɺ�С��ϵͳ��е���غ�,�ɻ�е���غ㶨�ɵã�
����̣����ɺ�С��ϵͳ��е���غ�,�ɻ�е���غ㶨�ɵã�
![]()
��ã�
![]()
(2)С���![]() ʱ�Ķ��ܣ�
ʱ�Ķ��ܣ�
![]()
��С��![]() ��ʱ�����С���������Ϊ
��ʱ�����С���������Ϊ![]() ����ţ�ٵڶ����ɵã�
����ţ�ٵڶ����ɵã�
![]()
��ã�
![]()
����ţ�ٵ������ɿɵ�С��![]() ��ʱ�Թ����ѹ��Ϊ
��ʱ�Թ����ѹ��Ϊ![]() ��������ֱ����
��������ֱ����
(3)С��ǡ��![]() ����������п�ֱ�ӻ��еײ�����������ȡ������������Сֵ����ƽ���˶����ɿɵã�
����������п�ֱ�ӻ��еײ�����������ȡ������������Сֵ����ƽ���˶����ɿɵã�
![]()
![]()
������ã�
![]()
С���ͷŵ�![]() �Ĺ����У��ݶ��ܶ���Ϊ��
�Ĺ����У��ݶ��ܶ���Ϊ��
![]()
��ã�
![]()
С��ֱ�ӻ���![]() ��ʱ����������ȡ�������������ֵ����ƽ���˶����ɿɵã�
��ʱ����������ȡ�������������ֵ����ƽ���˶����ɿɵã�
![]()
![]()
������ã�
![]()
С���ͷŵ�![]() �Ĺ����У��ݶ��ܶ���Ϊ��
�Ĺ����У��ݶ��ܶ���Ϊ��
![]()
��ã�
![]()
���Ϸ��������ĵ�������Ӧ���㣺
![]()