题目内容
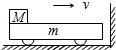质量m=1kg的小车左端放有质量M=3kg的铁块，两者以v0=4m/s的共同速度沿光滑水平面向竖直墙运动，车与墙的碰撞时间极短，无动能损失．铁块与车间的动摩擦因数为μ=1/3，车足够长，铁块不会到达车的右端．从小车第一次与墙相碰开始计时，取水平向右为正方向，g=10m/s2，求：（1）当小车和铁块再次具有共同速度时，小车右端离墙多远？
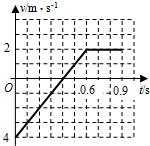
（2）在答卷的图上画出第二次碰撞前，小车的速度时间图象．不要求写出计算过程，需在图上标明图线的起点、终点和各转折点的坐标．
分析：根据动量守恒求共同速度，然后可以以小车为研究对象根据动能定理求右端离墙的距离；
小车先匀减速后反向匀加速，最后匀速，做出速度时间图象．
小车先匀减速后反向匀加速，最后匀速，做出速度时间图象．
解答：解：（1）撞墙后至两者具有共同速度，小车和铁块系统动量守恒：
（M-m）v0=（M+m）v1，
此时小车右端离墙距离s1，由动能定理知：-μMgs1=
m
-
m
，
解得：s1=0.6m．
（2）如图，要求：坐标系完整正确；
答：（1）当小车和铁块再次具有共同速度时，小车右端离墙0.6m远．
（2）如图．
（M-m）v0=（M+m）v1，
此时小车右端离墙距离s1，由动能定理知：-μMgs1=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 0 |
解得：s1=0.6m．
（2）如图，要求：坐标系完整正确；
答：（1）当小车和铁块再次具有共同速度时，小车右端离墙0.6m远．
（2）如图．
点评：本题考查了动量守恒与动能定理以及运动形式的分析，有一定难度．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
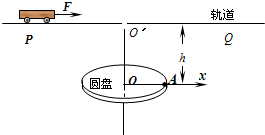（2011?淮安三模）如图所示，半径R=0.4m的圆盘水平放置，绕竖直轴OO′匀速转动，在圆心O正上方h=0.8m高处固定一水平轨道PQ，转轴和水平轨道交于O′点．一质量m=1kg的小车（可视为质点），在F=4N的水平恒力作用下，从O′左侧x0=2m处由静止开始沿轨道向右运动，当小车运动到O′点时，从小车上自由释放一小球，此时圆盘半径OA与x轴重合．规定经过O点水平向右为x轴正方向．小车与轨道间的动摩擦因数μ=0.2，g取10m/s2．求：
倾角为37°的光滑斜面上固定一个槽，劲度系数k=20N/m、原长l0=0.6m的轻弹簧下端与轻杆相连，开始时杆在槽外的长度l=0.3m，且杆可在槽内移动，杆与槽间的滑动摩擦力大小Ff=6N，杆与槽之间的最大静摩擦力等于滑动摩擦力．质量m=1kg的小车从距弹簧上端L=0.6m处由静止释放沿斜面向下运动．已知弹性势能Ep=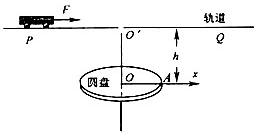
如图所示，半径R=0.2m的圆盘水平放置，绕竖直轴OO′匀速动转，在圆心O正上方h=0.8m高处固定一水平轨道PQ，转轴和水平轨道交于O′点．一质量m=1kg的小车（可视为质点），在F=4N的水平恒力作用下，从O′左侧x0=1m处由静止开始沿轨道向右运动，当小车运动到O′点时，从小车上自由释放一小球，此时圆盘半径OA与x轴重合．规定经过O点水平向右为x轴正方向．小车与轨道间的动摩擦因数μ=0.2，g取10m/s2．
如图，水平地面和半圆轨道面均光滑，质量M=1kg的小车静止在地面上，小车上表面与