题目内容
1.一个带正电的小物体,q=1×10-6C,放在绝缘的水平地面上,图甲中,空间若加上水平方向的变化电场,其加速度随电场力变化图象为图乙所示.现从静止开始计时,改用图丙中周期性变化的水平电场作用(g取10m/s2).求: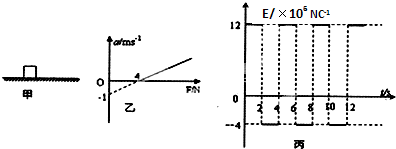
(1)物体的质量及物体与地面间的动摩擦因数;
(2)在图丙所示周期性变化的水平电场作用下,物体一个周期内的位移大小;
(3)在图丙所示周期性变化的水平电场作用下,23s内电场力对物体所做的功.
分析 (1)由牛顿第二定律结合图象乙解得;
(2)利用牛顿第二定律求出加速度,再利用运动学公式求出一个周期内的位移即可;
(3)通过周期性的运动过程求出23s内的位移,然后求出拉力做的功.
解答 解:(1)由牛顿第二定律得:F-μmg=ma
得:$a=\frac{1}{m}F\;-μg$
结合乙图象得:m=4kg;μ=0.1
(2)0~2s:由牛顿第二定律可得:F1-μmg=ma1
${a}_{1}=\frac{{F}_{1}-μmg}{m}=\frac{12-4}{4}m/{s}^{2}=2m/{s}^{2}$
前2s内通过的位移为:${x}_{1}=\frac{1}{2}{{a}_{1}t}_{1}^{2}=\frac{1}{2}×2×{2}^{2}m=4m$
2s~4s:由牛顿第二定律可得:F2-μmg=ma2
${a}_{2}=\frac{{F}_{2}-μmg}{m}=\frac{-4-4}{4}m/{s}^{2}=-2m/{s}^{2}$
2s~4s:物体做匀减速运动,t=4s时速度恰好为0,
由以上式可知:一个周期内的位移为x=2x1=8m
(3)23s内E1作用下位移为6x1,E2作用下位移为5x1+3m,
因此W1=E1q×6x1=288J
W2=-E2q×(5x1+3m)=-92J
即23s内电场力做功为:W=W1+W2=196J
答:(1)物体的质量为4kg,物体与地面间的动摩擦因数为0.1.
(2)求周期力作用下物体在一个周期内的位移大小为8m.
(3)23s内力F对物体所做的功为196J.
点评 本题涉及牛顿运动定律和运动学的知识以及运动定理的应用,求解本题的关键是认真分析物理过程,主要考查分析、推理和综合能力.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
9.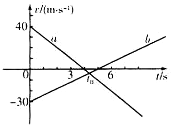 甲、乙两车同时从同一地点沿同一直线运动,其v-t图象分别如图中直线a、b所示,t0时刻两图线相交.由图可知( )
甲、乙两车同时从同一地点沿同一直线运动,其v-t图象分别如图中直线a、b所示,t0时刻两图线相交.由图可知( )
 甲、乙两车同时从同一地点沿同一直线运动,其v-t图象分别如图中直线a、b所示,t0时刻两图线相交.由图可知( )
甲、乙两车同时从同一地点沿同一直线运动,其v-t图象分别如图中直线a、b所示,t0时刻两图线相交.由图可知( )| A. | 两车的初速度方向相同 | B. | 两车的加速度大小相等 | ||
| C. | 0~6 s内,t0时刻两车相距最远 | D. | t0时刻两车相遇 |
16.已知地球质量为M,半径为R,自转周期为T,地球同步卫星质量为m,引力常量为G,有关同步卫星,下列表述正确的是( )
| A. | 卫星运行时受到的向心力大小为G$\frac{Mm}{{R}^{2}}$ | |
| B. | 卫星的运行速度小于第一宇宙速度 | |
| C. | 卫星运行的向心加速度小于地球表面的重力加速度 | |
| D. | 卫星距地面的高度为$\root{3}{\frac{GM{T}^{2}}{4{π}^{2}}}$ |
13.从某高处释放一石子,经过时间t从同一地点再释放一石子.不计空气阻力,下列说法正确的是( )
| A. | 落地前,两石子的间距始终保持不变 | |
| B. | 落地前,两石子的速度差将越来越大 | |
| C. | 两石子落地的时间差为t | |
| D. | 由于石子质量未知,以上说法均不正确 |
10.甲物体重力是乙物体重力的五倍,甲从H高处自由下落,乙从2H高处同时开始自由落下,在两物体下落过程中,下面几种说法正确的是( )
| A. | 同一时刻甲的速度比乙的速度大 | B. | 下落后1 s末,它们的速度相等 | ||
| C. | 各自下落1 m时,它们的速度相等 | D. | 下落过程中甲的加速度比乙的大 |
11.如图所示为在同一直线上运动的A、B两质点的x-t图象,由图可知以下说法正确的是( )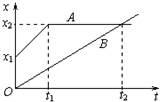

| A. | t=0时,A在B的前面x1处 | |
| B. | B在t2时刻追上A,并在此后跑在A的前面 | |
| C. | A在t1 到t2时间内做匀速直线运动 | |
| D. | t1时刻前B运动的速度比A小,但0到t2时间内B的平均速度比A大 |
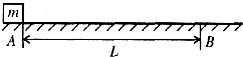 如图,质量m=2kg的物体静止于水平地面的A处,A、B间距L=20m.用大小为30N,方向水平向右的外力F0拉此物体,经t0=2s,拉至B处.
如图,质量m=2kg的物体静止于水平地面的A处,A、B间距L=20m.用大小为30N,方向水平向右的外力F0拉此物体,经t0=2s,拉至B处.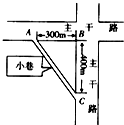 如图所示为某城市两条垂直相交的主干路的平面图,其中A、C两处各有一个公交站,AB=300m、BC=400cm,AC之间有一条小巷,某同学刚到A车站时,公交车恰好由静止启动,于是该同学立刻沿AC小巷奔跑,想赶上将在C处进站的该公交车.已知公交车在30s时间内能匀加速到14m/s,并以该速率行驶,进站时匀减速;且匀加速、匀减速的加速度大小相等,该同学奔跑中,匀减速过程加速度的大小是匀加速过程加速度大小的3倍,求该同学匀加速过程的加速度至少多大,才能在C点赶上该公交车?
如图所示为某城市两条垂直相交的主干路的平面图,其中A、C两处各有一个公交站,AB=300m、BC=400cm,AC之间有一条小巷,某同学刚到A车站时,公交车恰好由静止启动,于是该同学立刻沿AC小巷奔跑,想赶上将在C处进站的该公交车.已知公交车在30s时间内能匀加速到14m/s,并以该速率行驶,进站时匀减速;且匀加速、匀减速的加速度大小相等,该同学奔跑中,匀减速过程加速度的大小是匀加速过程加速度大小的3倍,求该同学匀加速过程的加速度至少多大,才能在C点赶上该公交车?