题目内容
2．
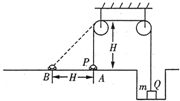如图所示，一辆汽车通过轻绳和定滑轮将竖井中质量为m的重物吊起，开始时左右两侧的绳处于竖直状态，且左侧的绳长为H，汽车静止不动，然后汽车向左行驶．当通过水平距离为H时、汽车的速度达到v，求此过程中绳的拉力对重物做了多少功．
分析 对B点的速度分解为沿绳子方向和垂直于绳子方向，在沿绳子方向的速度等于物体的速度，根据平行四边形定则求出物体的速度大小．从A到B的过程中，求出重物上升的高度，根据动能定理求出绳子拉力做功的大小．
解答 解：车与重物的速度关系如右图所示，物体的速度大小vcos45°=$\frac{\sqrt{2}}{2}$v，方向竖直向上；
设绳Q端对物体做功为W，由几何关系可得重物上升的高度为：h=（$\sqrt{2}$-1）H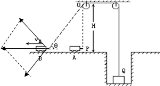
所以物体克服重力做功为：WG=mgh=mg（$\sqrt{2}$-1）H
对重物应用动能定理得：W-WG=$\frac{1}{2}$mv2
解得：W=$\frac{1}{4}$mv2+（$\sqrt{2}$-1）mgH
答：拉力对物体做的功W为$\frac{1}{4}$mv2+（$\sqrt{2}$-1）mgH．
点评 本题考查了动能定理和速度的合成和分解综合运用，难度中等，知道汽车沿绳子方向的分速度等于物体的速度．
练习册系列答案
相关题目
12．一辆小汽车在一段平直的公路上做匀加速直线运动，A、B是运动过程中经过的两点．已知汽车经过A点时的速度为1m/s，经过B点时的速度为7.0m/s„则汽车从A到B的运动过程中，下列说法中正确的是（ ）
| A． | 汽车经过AB段位移中点时速度是4m/s | |
| B． | 汽车经过AB段中间时刻的速度是5m/s2 | |
| C． | 汽车前一半位移所用时间是后一半位移所用时间的2倍 | |
| D． | 汽车前一半时间发生位移是后一半时间发生位移的一半 |
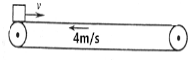如图，物体以12m/s的初速度冲上水平传送带左端，传送带长L=10m，以4m/s的恒定速率逆时针转动，已知物体与传动带间的动摩擦因数μ=0.4，求：物体在传送带上运动的时间．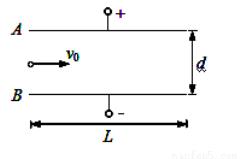
。
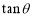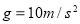，求：