题目内容
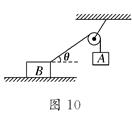
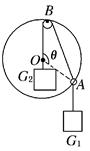
(12分)如图15所示，光滑小圆环A吊着一个重为G1的砝码套在另一个竖直放置的大圆环上，今有一细绳拴在小圆环A上，另一端跨过固定在大圆环最高点B处的一个小滑轮后吊着一个重为G2的砝码，如果不计小环、滑轮、绳子的重量大小．绳子又不可伸长，求平衡时弦AB所对的圆心角θ.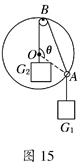
2arcsin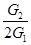
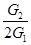
以小圆环A为研究对象，它受到的力有：竖直绳对它的拉力F1＝
G1，其方向竖直向下；AB绳对它的拉力F2＝G2，其方向沿AB方向；大
圆环对它的弹力FN，其方向沿半径指向圆外，在F1、F2、FN三力的共同作用下，小圆
环处于平衡状态．
将小圆环A所受的三个力利用力的合成和力的分解，组成三角形，如图所示．
由几何关系得△OAB与△FNAF2′相似，得
＝
＝
.
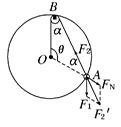
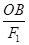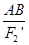所以FN＝F1，sin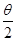
＝
，
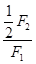将F1＝G1、F2＝G2代入
解得θ＝2arcsin.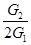
G1，其方向竖直向下；AB绳对它的拉力F2＝G2，其方向沿AB方向；大
圆环对它的弹力FN，其方向沿半径指向圆外，在F1、F2、FN三力的共同作用下，小圆
环处于平衡状态．
将小圆环A所受的三个力利用力的合成和力的分解，组成三角形，如图所示．
由几何关系得△OAB与△FNAF2′相似，得
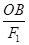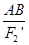＝＝.所以FN＝F1，sin
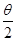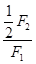＝，将F1＝G1、F2＝G2代入
解得θ＝2arcsin
.
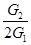练习册系列答案
名校课堂系列答案
相关题目
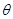
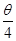
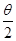
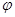多大？
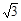∶1
