题目内容
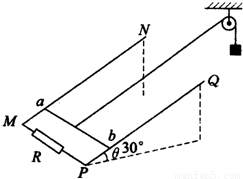
如图所示,足够长的光滑平行导轨MN、PQ倾斜放置,两导轨间距离为L=1.0m,导轨平面与水平面间的夹角为30°,磁感应强度为B的匀强磁场垂直于导轨平面向上,导轨的M、P两端连接阻值为R=3.0Ω的电阻,金属棒ab垂直于导轨放置并用细线通过光滑定滑轮与重物相连,金属棒ab的质量m=0.20kg,电阻r=0.50Ω,重物的质量M=0.60kg,如果将金属棒和重物由静止释放,金属棒沿斜面上滑的距离与时间的关系如下表所示,不计导轨电阻,g=10m/s2.求:(1)所加磁场的磁感应强度B为多大?
(2)电阻R在0.6s内产生的热量为多少?
| 时间t(s) | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | |
| 上滑距离(m) | 0.05 | 0.15 | 0.35 | 0.70 | 1.05 | 1.40 |
【答案】分析:(1)由表格中数据可知ab棒最终做匀速运动,受力平衡;由共点力的平衡条件可求得安培力的大小,即可求得磁感应强度;
(2)分析棒能量的转化方向,由能量的转化与守恒定律可求得产生的热量.
解答: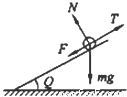 解:(1)由表中数据可以看出最终ab棒将匀速运动
解:(1)由表中数据可以看出最终ab棒将匀速运动
匀速运动速度: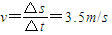
棒受力如图,由平衡条件可得
T=F+mgsin30°
T=Mg
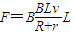
联立解得: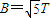
(2)在0.6s内通过的位移为s=1.40m,由能的转化守恒得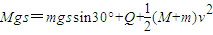
又因为: ⑦
⑦
联立解得:QR=1.8J ⑧
答:(1)磁感应强度为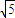 T;(2)电阻在0.6s内产生的热量为1.8J.
T;(2)电阻在0.6s内产生的热量为1.8J.
点评:本题考查电磁感应中的能量转化问题,要求学生能分析能量的转化方向,正确列出能量守恒关系.
(2)分析棒能量的转化方向,由能量的转化与守恒定律可求得产生的热量.
解答:
 解:(1)由表中数据可以看出最终ab棒将匀速运动
解:(1)由表中数据可以看出最终ab棒将匀速运动匀速运动速度:
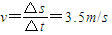
棒受力如图,由平衡条件可得
T=F+mgsin30°
T=Mg
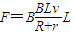
联立解得:
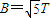
(2)在0.6s内通过的位移为s=1.40m,由能的转化守恒得
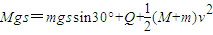
又因为:
 ⑦
⑦联立解得:QR=1.8J ⑧
答:(1)磁感应强度为
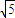 T;(2)电阻在0.6s内产生的热量为1.8J.
T;(2)电阻在0.6s内产生的热量为1.8J.点评:本题考查电磁感应中的能量转化问题,要求学生能分析能量的转化方向,正确列出能量守恒关系.

练习册系列答案
相关题目
 如图所示,在MN的下方足够大的空间是玻璃介质,其折射率为n=
如图所示,在MN的下方足够大的空间是玻璃介质,其折射率为n= (2010?资阳三模)如图所示,水平放置的两根足够长的平行光滑杆AB和CD,各穿有质量分别为M和m的小球,两杆之间的距离为d,两球用自由长度为d 的轻质弹簧连接,现从左侧用档板将M球挡住,再用力把m向左边拉一段距离(在弹性限度内)后自静止释放,释放后,下面判断中不正确的是( )
(2010?资阳三模)如图所示,水平放置的两根足够长的平行光滑杆AB和CD,各穿有质量分别为M和m的小球,两杆之间的距离为d,两球用自由长度为d 的轻质弹簧连接,现从左侧用档板将M球挡住,再用力把m向左边拉一段距离(在弹性限度内)后自静止释放,释放后,下面判断中不正确的是( ) (1)下列说法正确的是
(1)下列说法正确的是
