题目内容
【题目】如图所示,截面是扇形AOB的玻璃砖,半径为R,圆心角∠AOB=60°,一束单色光线与AO面成30°角,从AO面的C点射人玻璃砖,折射光线CD与OB面平行,且刚好从圆弧AB的中点D射出,光在真空中传播速度为c.求:

①单色光从C传播到D所用的时间;
②光线从D点出射后,与OB的延长线的交点离B点的距离.
【答案】(1)![]() (2)
(2)![]()
【解析】
①作光路图如图所示:
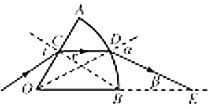
由几何关系可知,光线在AO边的入射角为i=60°,折射角为r=30°,
根据折射定律可知![]()
设CD边长为L,由几何关系可知,![]() ,
,![]()
因此光从C到D所用时间为![]()
②由几何关系可知,光在D点折射的入射角为30°,根据关路可逆可知,光在D点的折射角为α=30°,
根据几何关系可知![]()
因此,E点到B点的距离为![]()

练习册系列答案
相关题目
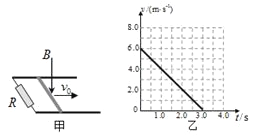
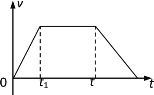
【题目】一位同学的家住在一座25层的高楼内,他每天乘电梯上楼,经过多次仔细观察和反复测量,他发现电梯启动后的运动速度符合如图所示的规律,他就根据这一特点在电梯内用台秤、重物和停表测量这座楼房的高度。他将台秤放在电梯内,将重物放在台秤的托盘上,电梯从第一层开始启动,经过不间断的运行,最后停在最高层。在整个过程中,他记录了台秤不同时间段内的示数。记录的数据如下表所示。
但由于0~3.0s段的时间太短,他没来得及将台秤的示数记录下来。假设在每个时间段内台秤示数都是稳定的。重力加速度g取10m/s2。
时间/s | 台秤示数/kg |
电梯启动前 | 5.0 |
0~3.0 | |
3.0~13.0 | 5.0 |
13.0~19.0 | 4.6 |
19.0以后 | 5.0 |
⑴电梯在0~3.0s时间段内台秤的示数应该是多少。
⑵根据测量的数据,计算该座楼房每一层的平均高度。