题目内容
2.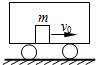 如图所示,设车厢长度为L,质量为M,静止于光滑的水平面上,车厢内有一质量为m 的物体以初速度v0向右运动,与车厢壁来回碰撞n次后,静止在车厢中.这时车厢的速度是( )
如图所示,设车厢长度为L,质量为M,静止于光滑的水平面上,车厢内有一质量为m 的物体以初速度v0向右运动,与车厢壁来回碰撞n次后,静止在车厢中.这时车厢的速度是( )| A. | v0,水平向右 | B. | 0 | ||
| C. | $\frac{m{v}_{0}}{M+m}$,水平向右 | D. | $\frac{m{v}_{0}}{M-m}$,水平向右 |
分析 物体与车厢反复碰撞,最终两者速度相等,在此过程中,两者组成的系统动量守恒,由动量守恒定律可以求出车厢的速度.
解答 解:以物体与车厢组成的系统为研究对象,以小球的初速度方向为正方向,由动量守恒定律可得:
mv0=(M+m)v,
最终车的速度:v=$\frac{m{v}_{0}}{M+m}$,方向与v的速度相同,水平向右;
故选:C.
点评 本题考查了求小车的速度,选物体与小车组成的系统为研究对象,水平方向仅有系统的内力作用而不受外力作用,故此方向满足动量守恒,碰撞前的动量,等于最后的总动量,典型的动量守恒的题目.

练习册系列答案
相关题目
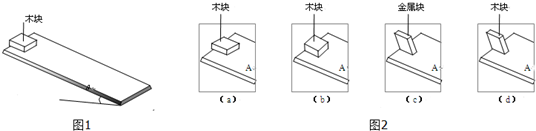
7.某小组同学试图探究物体从斜面顶端由静止下滑到底端时速度的大小v与哪些因素有关.他们猜想v可能与斜面的倾角θ、斜面材料、物体的质量m三个因素有关,于是选用:一长方体木块、100克砝码片(可粘在木块上表面)、两个长度相同材料不同的斜面A和B进行试验.按图1所示,将木块平放在斜面顶端,木块由静止下滑,用传感器测得其到达底端时的v.改变相关条件,多次试验,并将实验数据记录在表中:
1分析比较表中数据可得:v与物体质量无关.
②分析比较试验序号1、5、6、8与9的数据及相关条件,可得出的初步结论是:同一木块,平放在长度相同的斜面顶端由静止下滑,斜面倾角θ越大,物体滑到斜面底端时的速度越大.
③在试验序号7中:v7大于$\frac{358+438}{2}$厘米/秒(选填“大于”、“等于”或“小于”)
④完成上述试验后,有同学提出新的猜想:v可能还与物体跟斜面的接触面积有关.为了验证猜想,应选择图2中(d)与(a)进行对比试验[选填“(b)”、“(c)”或“(d)”],即可得出初步结论.
| 试验序号 | θ | 斜面 | m(g) | v(cm/s) |
| 1 | 20° | A | 200 | 245 |
| 2 | 20° | A | 300 | 245 |
| 3 | 20° | B | 200 | 153 |
| 4 | 20° | B | 300 | 153 |
| 5 | 25° | A | 200 | 307 |
| 6 | 30° | A | 200 | 358 |
| 7 | 35° | A | 200 | v7 |
| 8 | 40° | A | 200 | 438 |
| 9 | 45° | A | 200 | 470 |
②分析比较试验序号1、5、6、8与9的数据及相关条件,可得出的初步结论是:同一木块,平放在长度相同的斜面顶端由静止下滑,斜面倾角θ越大,物体滑到斜面底端时的速度越大.
③在试验序号7中:v7大于$\frac{358+438}{2}$厘米/秒(选填“大于”、“等于”或“小于”)
④完成上述试验后,有同学提出新的猜想:v可能还与物体跟斜面的接触面积有关.为了验证猜想,应选择图2中(d)与(a)进行对比试验[选填“(b)”、“(c)”或“(d)”],即可得出初步结论.

11.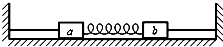 如图所示,将两相同的木块a、b置于粗糙的水平地面上,中间用一轻弹簧连接,两侧用细绳固定于墙壁.开始时a、b均静止,弹簧处于伸长状态,两细绳均有拉力,a所受摩擦力Ffa≠0,b所受摩擦力Ffb=0,现将右侧细绳剪断,则剪断瞬间( )
如图所示,将两相同的木块a、b置于粗糙的水平地面上,中间用一轻弹簧连接,两侧用细绳固定于墙壁.开始时a、b均静止,弹簧处于伸长状态,两细绳均有拉力,a所受摩擦力Ffa≠0,b所受摩擦力Ffb=0,现将右侧细绳剪断,则剪断瞬间( )
 如图所示,将两相同的木块a、b置于粗糙的水平地面上,中间用一轻弹簧连接,两侧用细绳固定于墙壁.开始时a、b均静止,弹簧处于伸长状态,两细绳均有拉力,a所受摩擦力Ffa≠0,b所受摩擦力Ffb=0,现将右侧细绳剪断,则剪断瞬间( )
如图所示,将两相同的木块a、b置于粗糙的水平地面上,中间用一轻弹簧连接,两侧用细绳固定于墙壁.开始时a、b均静止,弹簧处于伸长状态,两细绳均有拉力,a所受摩擦力Ffa≠0,b所受摩擦力Ffb=0,现将右侧细绳剪断,则剪断瞬间( )| A. | Ffa大小不变 | B. | Ffa方向改变 | C. | Ffb方向向右 | D. | Ffb仍然为零 |
12.下列说法正确的是( )
| A. | 温度升高,物体的每一个分子的动能都增大 | |
| B. | 外界对气体做功,气体的内能一定增大 | |
| C. | 当两个分子间的距离为r0(平衡位置)时,分子力为零,分子势能最小 | |
| D. | 布朗运动是悬浮在液体中固体颗粒分子的无规则运动 |

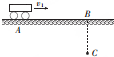 如图所示,公路上一辆汽车(可看成质点)以v1=12m/s的速度匀速行驶,汽车行至A点时,某人为搭车,从距公路30m远的C处开始以v2=3m/s的速度正对公路匀速跑去,司机见状途中刹车,汽车做匀减速直线运动,结果车停在B点时,人同时到达B点.已知A、B间的距离x=100m.试求:
如图所示,公路上一辆汽车(可看成质点)以v1=12m/s的速度匀速行驶,汽车行至A点时,某人为搭车,从距公路30m远的C处开始以v2=3m/s的速度正对公路匀速跑去,司机见状途中刹车,汽车做匀减速直线运动,结果车停在B点时,人同时到达B点.已知A、B间的距离x=100m.试求: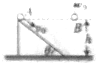 如图所示,小球A沿高为h,倾角为θ的光滑斜面以初速度v0从顶端滑到底端,而相同的小球B以同样的大小的初速度从同等高度处竖直上抛,不计空气阻力,则着地之前A、B两小球的加速度大小的比值为sinθ:1;A、B两小球着地时速度的竖直分量的比值为sinθ:1;着地时,A、B两小球的重力功率的比值为sinθ:1.
如图所示,小球A沿高为h,倾角为θ的光滑斜面以初速度v0从顶端滑到底端,而相同的小球B以同样的大小的初速度从同等高度处竖直上抛,不计空气阻力,则着地之前A、B两小球的加速度大小的比值为sinθ:1;A、B两小球着地时速度的竖直分量的比值为sinθ:1;着地时,A、B两小球的重力功率的比值为sinθ:1. 如图所示,一质量M=0.4kg的小物块B在足够长的光滑水平台面上静止不动,其右侧固定有一轻质水平弹簧(处于原长).台面的右边平滑对接有一等高的水平传送带,传送带始终以υ=1m/s的速率逆时针转动.另一质量m=0.1kg的小物块A以速度υ0=4m/s水平滑上传送带的右端.已知物块A与传送带之间的动摩擦因数μ=0.1,传送带左右两端的距离l=3.5m,滑块A、B均视为质点,忽略空气阻力,取g=10m/s2.
如图所示,一质量M=0.4kg的小物块B在足够长的光滑水平台面上静止不动,其右侧固定有一轻质水平弹簧(处于原长).台面的右边平滑对接有一等高的水平传送带,传送带始终以υ=1m/s的速率逆时针转动.另一质量m=0.1kg的小物块A以速度υ0=4m/s水平滑上传送带的右端.已知物块A与传送带之间的动摩擦因数μ=0.1,传送带左右两端的距离l=3.5m,滑块A、B均视为质点,忽略空气阻力,取g=10m/s2.