题目内容
17．
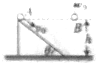如图所示，小球A沿高为h，倾角为θ的光滑斜面以初速度v0从顶端滑到底端，而相同的小球B以同样的大小的初速度从同等高度处竖直上抛，不计空气阻力，则着地之前A、B两小球的加速度大小的比值为sinθ：1；A、B两小球着地时速度的竖直分量的比值为sinθ：1；着地时，A、B两小球的重力功率的比值为sinθ：1．
分析 加速度根据牛顿第二定律求解．两个物体在运动的过程中机械能都守恒，可以求出它们落地时的速度大小，再得到再着地时速度的竖直分量的比值．由瞬时功率的公式可以求出着地时A、B两小球的重力功率的比值．
解答 解：A球的加速度 aA=$\frac{mgsinθ}{m}$=gsinθ，B球的加速度为 aB=g，则aA：aB=sinθ：1．
根据机械能守恒定律得：$\frac{1}{2}m{v}^{2}$=mgh+$\frac{1}{2}m{v}_{0}^{2}$，可知两球着地时速度大小相等，则A、B两小球着地时速度的竖直分量的比值为 vA：vB=vsinθ：v=sinθ：1
着地时，A、B两小球的重力功率的比值 PA：PB=mgvsinθ：mgv=sinθ：1．
故答案为：sinθ：1，sinθ：1，sinθ：1．
点评 在计算功率的时候，一定要注意公式的选择，P=$\frac{W}{t}$只能计算平均功率的大小，而P=Fv可以计算平均功率也可以是瞬时功率，取决于速度是平均速度还是瞬时速度．
练习册系列答案
考前必练系列答案
相关题目
7．下列光学现象的说法正确的是（ ）
| A． | 在水中绿光的传播速度比红光的小 | |
| B． | 光纤由内芯和外套两层组成，内芯的折射率比外套的小 | |
| C． | 在岸边观察水中的鱼，看到的深度比实际的深 | |
| D． | 分别用绿光和红光在同一装置上做双缝干涉实验，用红光时得到的条纹间距更窄 |
8．如图所示，琥珀经摩擦后能吸引羽毛，它们之间的吸引力主要是（ ）
| A． | 重力 | B． | 静电力 | C． | 弹力 | D． | 摩擦力 |
12．
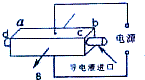电磁泵在目前的生产科技中得到了广泛应用．如图所示是电磁泵的原理图，泵体是一个长方体，ab边长为L，两侧端面是边长为a的正方形；流经泵体内的液体密度为ρ，在进口处接入电导率为σ（电阻率的倒数）的导电液，泵体所在处有方向垂直侧面向外的磁场B，泵体的上下两表面接在电压恒为U的电源上．则（ ）
电磁泵在目前的生产科技中得到了广泛应用．如图所示是电磁泵的原理图，泵体是一个长方体，ab边长为L，两侧端面是边长为a的正方形；流经泵体内的液体密度为ρ，在进口处接入电导率为σ（电阻率的倒数）的导电液，泵体所在处有方向垂直侧面向外的磁场B，泵体的上下两表面接在电压恒为U的电源上．则（ ）| A． | 泵体上表面应接电源正极 | |
| B． | 通过泵体的电流I=$\frac{UL}{σ}$ | |
| C． | 增大磁感应强度，每秒被抽液体的质量就越大 | |
| D． | 增大电导率σ，电磁驱动力所产生的附加压强越小 |
2．
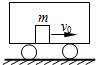如图所示，设车厢长度为L，质量为M，静止于光滑的水平面上，车厢内有一质量为m 的物体以初速度v0向右运动，与车厢壁来回碰撞n次后，静止在车厢中．这时车厢的速度是（ ）
如图所示，设车厢长度为L，质量为M，静止于光滑的水平面上，车厢内有一质量为m 的物体以初速度v0向右运动，与车厢壁来回碰撞n次后，静止在车厢中．这时车厢的速度是（ ）| A． | v0，水平向右 | B． | 0 | ||
| C． | $\frac{m{v}_{0}}{M+m}$，水平向右 | D． | $\frac{m{v}_{0}}{M-m}$，水平向右 |
9．核能作为一种新能源在现代社会中已不可缺少，我国在完善核电安全基础上将加大核电站建设．核泄漏中的钚（Pu）是一种具有放射性的超铀元素，它可破坏细胞基因，提高罹患癌症的风险．已知钚的一种同位素${\;}_{94}^{239}$Pu的半衰期为24100年，其衰变方程为${\;}_{94}^{239}$Pu→X+${\;}_{2}^{4}$He+γ，下列有关说法正确的是（ ）
| A． | X原子核中含有143个中子 | |
| B． | 100个${\;}_{94}^{239}$Pu经过24100年后一定还剩余50个 | |
| C． | 由于衰变时释放巨大能量，根据E=mc2，衰变过程总质量增加 | |
| D． | 衰变发出的γ放射线是波长很短的光子，具有很强的穿透能力 |
6．将质量为m的砝码置于水平圆盘边缘，圆盘半径为R，圆盘对砝码的最大静摩擦力是其重量的K倍．当圆盘绕通过圆心的竖直轴转动，转动角速度达到ω时，砝码开始滑动．则（ ）
| A． | ω与K成正比 | B． | ω与$\sqrt{K}$成正比 | C． | ω与Kg成正比 | D． | ω与Kmg成正比 |
7．由于通讯和广播等方面的需要，许多国家发射了地球同步轨道卫星，这些卫星的（ ）
| A． | 轨道半径可以不同 | B． | 角速度的大小可以不同 | ||
| C． | 加速度的大小可以不同 | D． | 质量可以不同 |