题目内容
12.图1是测量阻值约为几欧的未知电阻Rx的原理图,图中R0是定值电阻(5Ω),R1是电阻箱(0-99.9Ω),R是滑动变阻器.A1和A2是电流表,E是电源(电动势约4.5V,内阻很小)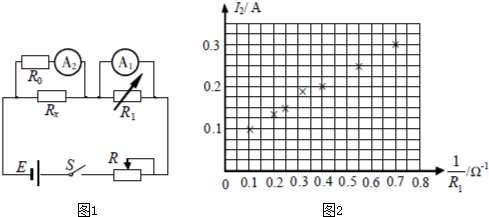
在保证安全和满足要求的情况下,使测量范围尽可能大,实验具体步骤如下:
(Ⅰ)连接好电路,将滑动变阻器R调到最大
(Ⅱ)闭合S,从零开始调节电阻箱R1为适当值,再调节滑动变阻器R,使A1示数I1=0.2A,记下这时电阻箱的阻值R1和A2的示数I2;
(Ⅲ)重复步骤(Ⅱ),再测量6组R1和I2值;
(Ⅳ)将实验测得的7组数据在坐标纸上描点;
根据实验回答以下问题:
①现有下列四个可供选用的电流表:
A.电流表(0-3mA内阻为 20.0Ω)
B.电流表(0-3mA内阻未知)
C.电流表(0-0.3A内阻未知)
D.电流表(0-0.3A内阻为5.0Ω)
电流表A1选C,电流表A2选D
②测得一组R1和I2值后,调整电阻箱R1使其阻值变小,要使A1示数仍为0.2A,应使滑动变阻器R接入电路的阻值变小(选填“不变”,“变大”或“变小”)
③在坐标纸上画出R1与I2的关系图.
④根据以上实验测得出Rx=6.0Ω.
分析 ①由题意可知,A1示数I1=0.2A,即可确定量程,根据题目中图象示数可知,A2的量程为0.3A;,
②根据电路规律可得出对应的电阻的变化;
③④根据串并联特征,结合R1与I2的图象的斜率含义,依据欧姆定律,即可求解.
解答 解:①A1示数I1=0.2A,则A1应选用量程为0.3A的电流表,由于只要知道电流大小即可,即选用C;
根据R1与I2的关系图,可知,A2的量程为0.3A,且必须要知道其电阻,因此选用D;
②调整电阻箱R1使其阻值变小,总电流增大;要使A1示数仍为0.2A,则应使滑动变阻器R接入电路分流增大;故其阻值应减小;
③根据题目中已知描的点,平滑连接,注意让图线分布在点的两边,删除错误的,如图所示;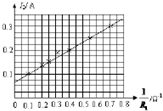
④(4)根据欧姆定律及串并联电路规律可知:
$\frac{{I}_{2}({R}_{0}+{R}_{A2})}{{R}_{x}}+{I}_{2}$=I1+$\frac{{I}_{1}{R}_{A1}}{{R}_{1}}$,
则有:
I2=$\frac{{R}_{x}{I}_{1}}{{R}_{0}+{R}_{A2}+{R}_{x}}$+$\frac{{R}_{x}{R}_{A1}}{{R}_{0}+{R}_{A2}+{R}_{x}}×\frac{1}{{R}_{1}}$$\frac{{R}_{x}{R}_{A1}}{{R}_{0}+{R}_{A2}+{R}_{x}}$;
由图象可知:$\frac{{R}_{x}{I}_{1}}{{R}_{0}+{R}_{A2}+{R}_{x}}$=0.075;$\frac{{R}_{x}{R}_{A1}}{{R}_{0}+{R}_{A2}+{R}_{x}}$=$\frac{0.3-0.1}{0.7-0.1}$=$\frac{1}{3}$
联立解得:
Rx=6.0Ω
故答案为:①C,D;②减小;③如图所示;④6.0
点评 本题考查如何确定电表的方法,紧扣题意是解题的关键,理解欧姆定律的应用,掌握串并联特点,注意误差与错误的区别,理解图象的斜率含义.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案| A. | 运动的时间t=$\frac{2{v}_{0}}{g}$ | B. | 瞬时速度vt=$\sqrt{5}$v0 | ||
| C. | 水平分速度与竖直分速度大小相等 | D. | 位移大小等于$\frac{2{{v}_{0}}^{2}}{g}$ |
| A. | 地球绕太阳公转的周期变为扩大前的2倍 | |
| B. | 地球绕太阳公转的周期与扩大前的相同 | |
| C. | 地球绕太阳公转的向心力变为扩大前的8倍 | |
| D. | 地球表面重力加速度变为扩大前的2倍 |
| A. | 在水中绿光的传播速度比红光的小 | |
| B. | 光纤由内芯和外套两层组成,内芯的折射率比外套的小 | |
| C. | 在岸边观察水中的鱼,看到的深度比实际的深 | |
| D. | 分别用绿光和红光在同一装置上做双缝干涉实验,用红光时得到的条纹间距更窄 |
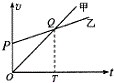 甲、乙两车在一平直道路上同向运动,其v-t图象如图所示,图中△OPQ和△OQT的面积分别为S1和S2(S2>S1),计时开始时,甲、乙两车相距S0,在两车运动过程中,下列说法正确的是( )
甲、乙两车在一平直道路上同向运动,其v-t图象如图所示,图中△OPQ和△OQT的面积分别为S1和S2(S2>S1),计时开始时,甲、乙两车相距S0,在两车运动过程中,下列说法正确的是( )| A. | 若甲车在乙车前方且S0=S1+S2,两车相遇1次 | |
| B. | 若甲车在乙车前方且S0<S1,两车相遇2次 | |
| C. | 若乙车在甲车前方且S0=S2,两车不会相遇 | |
| D. | 若乙车在甲车前方且S0=S1,甲车追上乙前T时刻相距最近 |
| A. | q$\sqrt{\frac{2k}{F}}$ | B. | $\sqrt{q\frac{k}{F}}$ | C. | 2q$\sqrt{\frac{k}{F}}$ | D. | 2q$\sqrt{\frac{F}{k}}$ |
| A. | 月球的半径 | B. | “嫦娥三号”的轨道半径 | ||
| C. | 月球的公转周期 | D. | “嫦娥三号”的公转周期 |
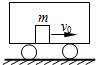 如图所示,设车厢长度为L,质量为M,静止于光滑的水平面上,车厢内有一质量为m 的物体以初速度v0向右运动,与车厢壁来回碰撞n次后,静止在车厢中.这时车厢的速度是( )
如图所示,设车厢长度为L,质量为M,静止于光滑的水平面上,车厢内有一质量为m 的物体以初速度v0向右运动,与车厢壁来回碰撞n次后,静止在车厢中.这时车厢的速度是( )| A. | v0,水平向右 | B. | 0 | ||
| C. | $\frac{m{v}_{0}}{M+m}$,水平向右 | D. | $\frac{m{v}_{0}}{M-m}$,水平向右 |
 有一定值电阻与电压为U的交流电源接通,结果通过电阻的电流为I.若通过一台变压器将该交流电与该电阻接通,已知变压器初级线圈中电流大小为$\frac{I}{4}$,则通过该电阻的电流I′=$\frac{I}{2}$;当变压器次级线圈所接电阻为原定值电阻的4倍时,那么这个电阻的电功率为$\frac{UI}{16}$.
有一定值电阻与电压为U的交流电源接通,结果通过电阻的电流为I.若通过一台变压器将该交流电与该电阻接通,已知变压器初级线圈中电流大小为$\frac{I}{4}$,则通过该电阻的电流I′=$\frac{I}{2}$;当变压器次级线圈所接电阻为原定值电阻的4倍时,那么这个电阻的电功率为$\frac{UI}{16}$.