题目内容
一根对称的“∧”形玻璃管置于竖直平面内，管所有空间有竖直向上的匀强电场，带正电的小球在管内从A点由静止开始运动，且与管壁的动摩擦因数为μ，小球在B端与管作用时无能量损失，管与水平面间夹角为θ，AB长L，如右图所示，求从A开始，小球运动的总路程是多少？（设小球受的电场力大于重力）
解析
解析
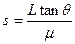
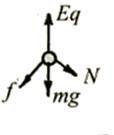
小球小球从A端开始运动后共受四个力作用，电场力为qE、重力mg、管壁支持力N、摩擦力f，由于在起始点A小球处于不平衡状态，因此在斜管上任何位置都是不平衡的，小球将做在“∧”管内做往复运动，最后停在B处。若以整个运动过程为研究对象，将使问题简化。
以小球为研究对象，受力如右图所示，由于电场力和重力做功与路径无关，
而摩擦力做功与路径有关，设小球运动的
总路程为s，由动能定理得：
qELsinθ—mgLsinθ－fs="0 " ①
又因为f=μN ②
N=(qE－mg)cosθ
所以由以上三式联立可解得小球运动的总路程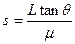： ③
|
而摩擦力做功与路径有关，设小球运动的
总路程为s，由动能定理得：
qELsinθ—mgLsinθ－fs="0 " ①
又因为f=μN ②
N=(qE－mg)cosθ
所以由以上三式联立可解得小球运动的总路程：
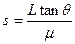③
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
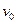沿垂直于电场线方向进入电容器，恰能从下边缘处飞出，飞出时速度大小为
，若其他条件不变，而在电容器内加上垂直纸面向里的匀强磁场，则带电粒子恰能从上极板边缘处飞出，飞出时速度大小为
，不计粒子的重力，则以下速度大小的关系正确的是（ ）
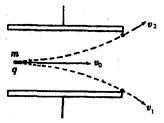
kg，电荷量q=9×