题目内容
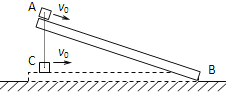
【题目】如图,水平面上的矩形箱子内有一倾角为θ的固定斜面,斜面上放一质量为m的光滑球,静止时,箱子顶部与球接触但无压力,箱子由静止开始向右做匀加速运动,然后该做加速度大小为a的匀减速运动直至静止,经过的总路程为s,运动过程中的最大速度为v.
(1)求箱子加速阶段的加速度为a′.
(2)若a>gtanθ,求减速阶段球受到箱子左壁和顶部的作用力.
【答案】(1)![]() (2)macotθ﹣mg
(2)macotθ﹣mg
【解析】
试题分析:(1)设加速度为a′,由匀变速直线运动的公式:![]()
![]()
得:![]()
解得: ![]()
(2)设小球不受车厢的作用力,应满足:Nsinθ=ma
Ncosθ=mg
解得:a=gtanθ
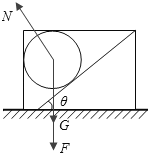
减速时加速度的方向向左,此加速度有斜面的支持力N与左壁支持力共同提供,当a>gtanθ 时,
左壁的支持力等于0,此时小球的受力如图,则:Nsinθ=ma
Ncosθ﹣F=mg
解得:F=macotθ﹣mg

练习册系列答案
相关题目