Question

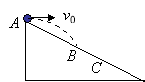
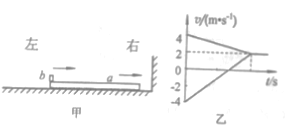
【题目】如图甲所示，在光滑水平面上有一木板a，木板上有木块b（可视为质点），二者以相同的速度向右运动。木板a与竖直墙壁发生碰撞后，立即以碰撞前的速度大小反向弹回，取反向弹回时t=0，此后二者的速度v随时间t变化的情况如图乙所示，已如木板a的质量大于木块b的质量，且木板a的质量m1=3.0kg，则

A. a、b相互作用后，二者一起运动的方向一定水平向左

B. 木块b的质量m2=2.0kg

C. 木板与墙壁碰撞后的运动过程摩擦力对b做功为-6J

D. 木板与墙壁碰撞后的运动过程中系统损失的机械能Δ E=24 J

Answer 1

【答案】ACD

【解析】由图可知木板a与墙壁碰撞后速度方向水平向左，大小为4m/s，木块b的速度向右，大小为-4m/s，取向左为正方向，当二者一起运动时速度为2m/s向左，选项A正确；由动量守恒定律，结合图像可知： ，且m1=3.0kg，解得m2=1.0kg，选项B错误；根据动能定理，木板与墙壁碰撞后的运动过程摩擦力对b做功为，选项C正确；木板与墙壁碰撞后的运动过程中系统损失的机械能，选项D正确；故选ACD.