题目内容
18.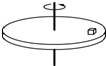 如图所示,置于圆形水平转台上的小物块随转台转动.若转台以角速度ω0=2rad/s.转动时,物块恰好与平台发生相对滑动.现测得小物块与转轴间的距离l1=0.50m,设物块所受的最大静摩擦力等于滑动摩擦力,重力加速度g取10m/s2.
如图所示,置于圆形水平转台上的小物块随转台转动.若转台以角速度ω0=2rad/s.转动时,物块恰好与平台发生相对滑动.现测得小物块与转轴间的距离l1=0.50m,设物块所受的最大静摩擦力等于滑动摩擦力,重力加速度g取10m/s2.(1)求小物块与转台间的摩擦因数.
(2)若小物块与转轴间距离变为l2=1.0m,则水平转台转动的角速度最大为多少?
分析 1、小物块随转台匀速转动过程中,受到竖直向下的重力、竖直向上的支持力、以及指向圆心的静摩擦力,其中静摩擦力f提供向心力.
2、小物块恰好发生相对滑动,它所受的摩擦力f=μmg,根据牛顿第二定律有f=mω2l,即μmg=mω2l,化简可得角速度的值.
解答 解:(1)恰好发生相对滑动时由最大静摩擦力提供圆周运动向心力:
f=μmg=mω02l1
解得:μ=0.2
(2)转动半径变为l2时有:
μmg=mωm2l2
解得:ωm=$\sqrt{2}$rad/s.
答:(1)小物块与转台间的摩擦因数是0.2.
(2)若小物块与转轴间距离变为l2=1.0m,则水平转台转动的角速度最大为$\sqrt{2}$rad/s.
点评 本题要能够正确的受力分析,知道是静摩擦力提供的向心力,根据牛顿第二定律列式求解.

练习册系列答案
相关题目
13.放在光滑水平面上的物体,受到和水平面成60°角的斜向上的拉力作用2s钟,获得动量为40kg•m/s(物体没有离开地面).这个拉力大小为( )
| A. | 80N | B. | 40N | C. | 34.6N | D. | 20N |
3.下列哪些做法能使线圈中产生感应电流?( )
| A. | 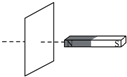 磁铁靠近或远离线圈 | |
| B. | 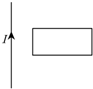 线圈远离或靠近通电导线 | |
| C. | 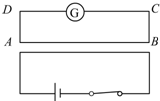 下边电路中通有恒定电流 | |
| D. | 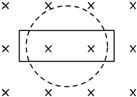 匀强磁场中,周长一定的闭合线圈由矩形变为圆形 |
7.如图甲所示,为测定物体冲上粗糙斜面能达到的最大位移x与斜面倾角θ的关系,将某一物体每次以不变的初速率v0沿足够长的斜面向上推出,调节斜面与水平方向的夹角θ,实验测得x与斜面倾角θ的关系如图乙所示,g取10m/s2,根据图象可求出( )
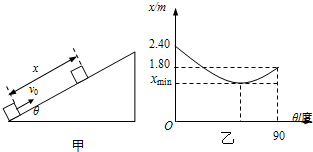

| A. | 物体的初速率6m/s,与斜面间的动摩擦因数μ=0.75 | |
| B. | 当θ=45°时,物体到最高点后将静止在斜面上 | |
| C. | 当θ=45°时,物体在斜面上滑行的位移x最小 | |
| D. | 物体在斜面上能达到的位移x的最小值为xmin=1.44m |
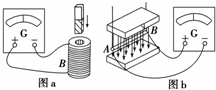 如图所示,高二10班物理研究性小组完成了以下两个演示实验,请你根据所学知识回答下列问题.
如图所示,高二10班物理研究性小组完成了以下两个演示实验,请你根据所学知识回答下列问题.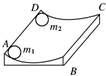 如图所示,一个光滑的圆弧形槽半径为R,圆弧所对的圆心角小于5°.AD的长为s,今有一小球m1以沿AD方向的初速度v从A点开始运动,要使小球m1可以与固定在D点的小球m2相碰撞,那么小球m1的速度v应满足什么条件?
如图所示,一个光滑的圆弧形槽半径为R,圆弧所对的圆心角小于5°.AD的长为s,今有一小球m1以沿AD方向的初速度v从A点开始运动,要使小球m1可以与固定在D点的小球m2相碰撞,那么小球m1的速度v应满足什么条件?