ЬтФПФкШн
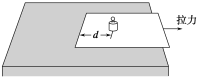
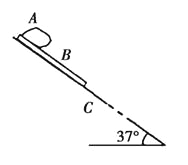
ЁОЬтФПЁПШчЭМЫљЪОЃЌЧуНЧЮЊ37ЁуЃЌГЄЮЊl=16mЕФДЋЫЭДјЃЌзЊЖЏЫйЖШЮЊv=10m/sЃЌЖЏФІВСвђЪ§ІЬ=0.5ЃЌдкДЋЫЭДјЖЅЖЫAДІЮоГѕЫйЖШЕиЪЭЗХвЛИіжЪСПЮЊm=0.5kgЕФЮяЬхЃЎвбжЊsin 37Ёу=0.6ЃЌcos 37Ёу=0.8ЃЌg=10m/s2 ЃЎ ЧѓЃК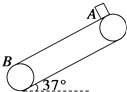
ЃЈ1ЃЉДЋЫЭДјЫГЪБеызЊЖЏЪБЃЌЮяЬхДгЖЅЖЫAЛЌЕНЕзЖЫBЕФЪБМфЃЛ
ЃЈ2ЃЉДЋЫЭДјФцЪБеызЊЖЏЪБЃЌЮяЬхДгЖЅЖЫAЛЌЕНЕзЖЫBЕФЪБМфЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКДЋЫЭДјЫГЪБеызЊЖЏЪБЃЌЮяЬхЯрЖдДЋЫЭДјЯђЯТдЫЖЏЃЌдђЮяЬхЫљЪмЛЌЖЏФІВССІбиаБУцЯђЩЯЃЌЯрЖдДЋЫЭДјЯђЯТдШМгЫйдЫЖЏЃЌгЩХЃЖйЕкЖўЖЈТЩЕУЃК
mgЃЈsin 37ЁуЉІЬcos 37ЁуЃЉ=maЃЌ
ДњШыЪ§ОнЕУЃКa=2m/s2ЃЌ
гЩдШБфЫйдЫЖЏЕФЮЛвЦЙЋЪНЕУЃКl= ![]() at2ЃЌ
at2ЃЌ
ДњШыЪ§ОнЕУЃКt=4 sЃЎ
Д№ЃКШєДЋЫЭДјЫГЪБеызЊЖЏЃЌЮяЬхгЩAЛЌЕНBЕФЪБМфЮЊ4sЃЎ
ЃЈ2ЃЉНтЃКДЋЫЭДјФцЪБеызЊЖЏЃЌЕБЮяЬхЯТЛЌЫйЖШаЁгкДЋЫЭДјзЊЖЏЫйЖШЪБЃЌЮяЬхЯрЖдДЋЫЭДјЯђЩЯдЫЖЏЃЌдђЮяЬхЫљЪмЛЌЖЏФІВССІбиДЋЫЭДјЯђЯТЃЌЩшЮяЬхЕФМгЫйЖШДѓаЁЮЊa1ЃЌгЩХЃЖйЕкЖўЖЈТЩЕУЃК
mgsin 37Ёу+ІЬmgcos 37Ёу=ma1ЃЌ
ДњШыЪ§ОнЕУЃКa1=10 m/s2ЃЌ
ЩшЕБЮяЬхдЫЖЏЫйЖШЕШгкДЋЫЭДјзЊЖЏЫйЖШЪБОРњЕФЪБМфЮЊt1ЃЌЮЛвЦЮЊx1ЃЌдђгаЃК
t1= ![]() =
= ![]() s=1 sЃЌ
s=1 sЃЌ
x1= ![]() a1t12=5 mЃМl=16 mЃЌ
a1t12=5 mЃМl=16 mЃЌ
ЕБЮяЬхдЫЖЏЫйЖШЕШгкДЋЫЭДјЫйЖШЫВМфЃЌгаmgsin 37ЁуЃОІЬmgcos 37ЁуЃЌ
дђЯТвЛЪБПЬЮяЬхЯрЖдДЋЫЭДјЯђЯТдЫЖЏЃЌЪмЕНДЋЫЭДјЯђЩЯЕФЛЌЖЏФІВССІЉЉФІВССІЗЂЩњЭЛБфЃЎ
ЩшЕБЮяЬхЯТЛЌЫйЖШДѓгкДЋЫЭДјзЊЖЏЫйЖШЪБЮяЬхЕФМгЫйЖШЮЊa2ЃЌгЩХЃЖйЕкЖўЖЈТЩЕУЃК
a2= ![]() ЃЌ
ЃЌ
ДњШыЪ§ОнЕУЃКa2=2 m/s2ЃЌ
ЮЛвЦЃКx2=lЉx1=16Љ5=11mЃЌ
гжвђЮЊx2=vt2+ ![]() a2t22ЃЌдђгаЃК10t2+t22=11ЃЌ
a2t22ЃЌдђгаЃК10t2+t22=11ЃЌ
НтЕУЃКt2=1 sЃЈt2=Љ11 sЩсШЅЃЉ
ЫљвдгаЃКtзм=t1+t2=2 sЃЎ
Д№ЃКШєДЋЫЭДјФцЪБеызЊЖЏЃЌЮяЬхДгAЕНBашвЊЕФЪБМфЮЊ2sЃЎ
ЁОНтЮіЁПЃЈ1ЃЉИєРыЗЈбЁШЁаЁЮяПщЮЊбаОПЖдЯѓНјааЪмСІЗжЮіЃЌШЛКѓгЩХЃЖйЕкЖўЖЈТЩЧѓаЁЮяПщЕФМгЫйЖШЃЌШЛКѓгЩдЫЖЏбЇЙЋЪНЧѓНтЃЎЃЈ2ЃЉЮяЬхдкДЋЫЭДјЩЯЪмЕНжиСІЁЂжЇГжСІКЭФІВССІзїгУЯШзіГѕЫйЖШЮЊ0ЕФдШМгЫйжБЯпдЫЖЏЃЌЕБЫйЖШКЭДЋЫЭДјЫйЖШвЛбљЪБНјааХаЖЯЮяЬхИњЫцДЋЫЭДјдШЫйЛЙЪЧЕЅЖРзідШБфЫйжБЯпдЫЖЏЃЌИљОнзмЮЛвЦЮЊ16mЃЌПЩвдЧѓГіећИідЫЖЏЙ§ГЬЕФЪБМфtЃЎ