题目内容
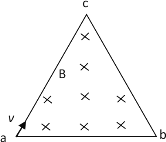
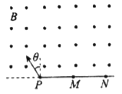
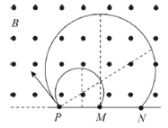
【题目】如图所示，直线边界PMN上方有足够大的匀强磁场B，方向垂直纸面向外，边界P点有一粒子源，以与竖直方向成θ角的不同速率向磁场中射入两个相同的粒子甲和乙，粒子甲、乙经磁场偏转后分别从边界上M、N点出磁场。已知PM＝MN，粒子重力不计，则甲、乙在磁场中运动的速度大小之比和甲、乙在磁场中运动的时间之比分别为（ ）
A.1：4，1：1B.1：4，1：4C.1：2，1：1D.1：2，1：4
【答案】C
【解析】
如图所示，粒子进入磁场时速度的垂线与PM的垂直平分线的交点为粒子甲在磁场做圆周运动的圆心，同理，粒子进入磁场时速度的垂线与PN的垂直平分线的交点为粒子乙在磁场中做圆周运动的圆心，由几何关系可知，两个粒子在磁场中做圆周运动的半径之比为
，由
可知，甲、乙的速度大小之比为
；由于粒子在磁场中做圆周运动的周期均为
，且两粒子在磁场中做圆周运动的轨迹所对的圆心角相同，因此粒子在磁场中运动的时间相同，甲、乙在磁场中运动的时间之比为
。
故选C．
练习册系列答案
导学与测试系列答案
新非凡教辅冲刺100分系列答案
相关题目
