题目内容
【题目】用与水平方向夹角为30°的倾斜传送带将质量为0.2kg的小煤块从高处运往低处,传送带两皮带轮轴心间的距离为L=22m,若传送带不动,将煤块从传送带顶端无初速度释放,滑到底端需用时4.69s(4.69≈![]() ).(g=10m/s2)求:
).(g=10m/s2)求:
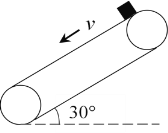
(1)煤块与传送带之间的滑动摩擦力大小;
(2)现让传送带的两轮逆时针转动,使传送带保持以4m/s的速度运行,将煤块无初速度地放到传送带顶端,求煤块到达传送带底端所用的时间。并求出此种情况下煤块在传送带上留下的黑色痕迹长度.
【答案】(1)0.6N (2)9m
【解析】
对煤块进行受力分析,开始时,受到重力、支持力、滑动摩擦力,处于加速阶段;当速度等于传送带速度时,根据重力的下滑分力与最大静摩擦力的关系,分析煤块能否匀速下滑,否则,继续加速.根据位移公式求解时间和划痕.
(1)皮带静止,煤块做初速度为零的匀加速直线运动,由![]()
可得a=2m/s2
根据物体的受力分析可得mgsinθ-f=ma
所以f=0.6N
(2)第一阶段:物体和传送带达同速前mgsinθ+f=ma1
可得a1=8m/s2
![]()
![]()
第二阶段:物体和传送带达共速后,因f<mgsinθ,物体仍将加速下滑
mgsinθ-f=ma2
可得a2=2m/s2
x2=L-x1=21m
![]()
可得t2=3s
t总=t2+t1=3.5s
第一阶段物体与传送带的相对位移△x1=vt1-x1=1m,物体相对传送带向后运动.
第一阶段物体与传送带的相对位移△x2=x2-vt2=9m,物体相对传送带向前运动,覆盖之前的痕迹.
所以划痕长度△x=9m

练习册系列答案
相关题目