题目内容
如图所示，一个人用一根长1m，只能承受46N拉力的绳子，拴着一个质量为1㎏的小球，在竖直平面内作圆周运动，已知圆心O离地面h=6m．转动中小球在最底点时绳子断了，（g=10m/s2）求：
（1）绳子断时小球运动的线速度多大？
（2）绳断后，小球落地点与抛出点间的水平距离．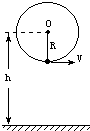
（1）绳子断时小球运动的线速度多大？
（2）绳断后，小球落地点与抛出点间的水平距离．
（1）最低点，小球受重力和拉力，合力充当向心力，根据牛顿第二定律，有：
Tm-mg=m
，
带入数据解得：v=
=
=6m/s；
（2）绳断后，小球做平抛运动，根据平抛运动的分位移公式，有
x=vt
y=
gt2
联立解得
x=v0
=6m
答：（1）绳子断时小球运动的线速度为6m/s；
（2）绳断后，小球落地点与抛出点间的水平距离为6m．
Tm-mg=m
| v2 |
| r |
带入数据解得：v=
|
|
（2）绳断后，小球做平抛运动，根据平抛运动的分位移公式，有
x=vt
y=
| 1 |
| 2 |
联立解得
x=v0
|
答：（1）绳子断时小球运动的线速度为6m/s；
（2）绳断后，小球落地点与抛出点间的水平距离为6m．
练习册系列答案
春雨教育同步作文系列答案
相关题目
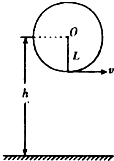如图所示，一个人用一根长L=lm，最大只能承受T=74N拉力的绳子，拴着一个质量m=1kg的小球，在竖直平面内做圆周运动．已知圆心O离地面的高度h=6m，g=10m/s2．求：
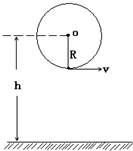如图所示，一个人用一根长1m，只能承受46N拉力的绳子，拴着一个质量为1kg的小球，在竖直平面内做圆周运动．已知圆心O离地面h=6m，转动中小球在最低点时绳子断了．
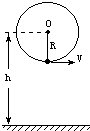如图所示，一个人用一根长1m，只能承受46N拉力的绳子，拴着一个质量为1㎏的小球，在竖直平面内作圆周运动，已知圆心O离地面h=6m．转动中小球在最底点时绳子断了，（g=10m/s2）求：
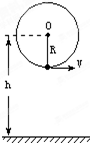如图所示，一个人用一根长为R=1米，能承受最大拉力为F=74N的绳子，系着一个质量为m=1Kg的小球，在竖直平面内作圆周运动，已知圆心O离地面高h=6米．运动中小球在圆周的最低点时绳子刚好被拉断，绳子的质量和空气阻力均忽略不计，g=10m/s2．求：
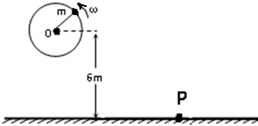如图所示，一个人用一根长L=1m，只能承受T=46N拉力的绳子，拴着一个质量为m=1kg的小球，在竖直面内做逆时针方向的圆周运动，已知圆心O离地的距离H=6m，g=10m/s2．