题目内容
(18分)如图在xoy平面内有平行于x轴的两个足够大的荧光屏M、N,它们的位置分别满足y=l和y=0,两屏之间为真空区域。在坐标原点O有一放射源不断沿y轴正方向向真空区域内发射带电粒子,已知带电粒子有两种。为探索两种粒子的具体情况,我们可以在真空区域内控制一个匀强电场和一个匀强磁场,电场的场强为E,方向与x轴平行,磁场的磁感应强度为B,方向垂直于xoy平面。
试验结果如下:如果让电场和磁场同时存在,我们发现粒子束完全没有偏转,仅在M屏上有一个亮点,其位置在S( 0 , l );如果只让磁场存在,我们发现仅在N屏上出现了两个亮点,位置分别为P( -2l , 0 )、Q( ,0 ),由此我们可以将两种粒子分别叫做P粒子和Q粒子。已知粒子间的相互作用和粒子重力可以忽略不计,试求(坐标结果只能用l表达):
,0 ),由此我们可以将两种粒子分别叫做P粒子和Q粒子。已知粒子间的相互作用和粒子重力可以忽略不计,试求(坐标结果只能用l表达):

(1)如果只让磁场存在,但将磁场的磁感应强度减为B1= ,请计算荧光屏上出现的所有亮点的位置坐标;
,请计算荧光屏上出现的所有亮点的位置坐标;
(2)如果只让电场存在,请计算荧光屏上出现的所有亮点的位置坐标;
(3)如果只让磁场存在,当将磁场的磁感应强度变为B2= kB时,两种粒子在磁场中运动的时间相等,求k的数值。
试验结果如下:如果让电场和磁场同时存在,我们发现粒子束完全没有偏转,仅在M屏上有一个亮点,其位置在S( 0 , l );如果只让磁场存在,我们发现仅在N屏上出现了两个亮点,位置分别为P( -2l , 0 )、Q(
 ,0 ),由此我们可以将两种粒子分别叫做P粒子和Q粒子。已知粒子间的相互作用和粒子重力可以忽略不计,试求(坐标结果只能用l表达):
,0 ),由此我们可以将两种粒子分别叫做P粒子和Q粒子。已知粒子间的相互作用和粒子重力可以忽略不计,试求(坐标结果只能用l表达):
(1)如果只让磁场存在,但将磁场的磁感应强度减为B1=
 ,请计算荧光屏上出现的所有亮点的位置坐标;
,请计算荧光屏上出现的所有亮点的位置坐标;(2)如果只让电场存在,请计算荧光屏上出现的所有亮点的位置坐标;
(3)如果只让磁场存在,当将磁场的磁感应强度变为B2= kB时,两种粒子在磁场中运动的时间相等,求k的数值。
(1)P粒子亮点位置(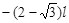 ,l ) Q粒子仍打在N屏上,易得亮点位置(l,0)
,l ) Q粒子仍打在N屏上,易得亮点位置(l,0)
(2)( ,l)、(-2l,l) (3)
,l)、(-2l,l) (3)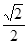
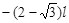 ,l ) Q粒子仍打在N屏上,易得亮点位置(l,0)
,l ) Q粒子仍打在N屏上,易得亮点位置(l,0)(2)(
 ,l)、(-2l,l) (3)
,l)、(-2l,l) (3)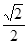
试题分析:(1)当磁场B和电场E同时存在时,两种粒子都受力平衡,都满足
Eq=Bqv
所以两种粒子速度相同都为v=
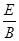 ①(2分)
①(2分)当仅存在磁场时,带电粒子做匀速圆周运动,洛仑兹力充当向心力,两种粒子都满足
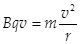 得
得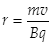 ②(2分)
②(2分)当磁场强度为B时,
P粒子的轨道半径r1=l,Q粒子轨道半径为r2=
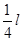 ③
③由②可知当磁场为B1减半时,两粒子做圆周运动的半径都加倍,此时 r1′=2l,r2′=

此时P粒子将打在M屏上,由几何关系可求出落点横坐标
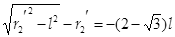
所以P粒子亮点位置(
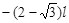 ,l ) (1分)
,l ) (1分)而Q粒子仍打在N屏上,易得亮点位置(l,0) (1分)
(2)由上问①②③式,可得两粒子的荷质比及其与E、B的关系,对P、Q分别有
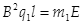 ④
④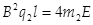 ⑤(1分)
⑤(1分)当仅存在电场时,P粒子将向右偏,y方向分运动为匀速直线运动
vt=l ⑥(1分)
x方向分运动为受电场力下的匀加速直线运动,有
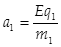 ⑦
⑦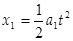 ⑧(1分)
⑧(1分)结合④⑥⑦可得
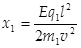 ⑨(1分)
⑨(1分)由①④⑨可得
x1=

同理可以求得Q粒子在-x方向的偏转位移为
x2=2l
故P、Q两粒子打在屏上的位置坐标分别为(
 ,l)、(-2l,l)。 (2分)
,l)、(-2l,l)。 (2分)(3)由②和③可以得出结论,不论磁场为多少,P、Q两粒子的轨道半径R1:R2=4:1不变。因为两粒子速度大小相等,所以要想两粒子运动时间相等,即运动弧长相等,两粒子运动的圆弧圆心角之比必须为θ1:θ2=1:4。
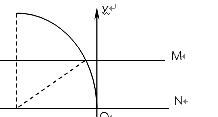
如图粒子打在M屏上时,其运动轨迹圆弧圆心角θ(锐角)与半径R满足l=Rsinθ,不可能满足R1:R2=4:1和θ1:θ2=1:4。所以两粒子都打在M屏上不可能满足要求。 (2分)
两粒子都打在N屏上,圆心角都为π也不能满足要求。 (2分)
所以结果必然为P粒子打在M屏而Q粒子打在N屏,所以θ2=π,而θ1=
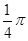 。
。由几何关系易得此时R1=
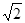 l,结合②③可求得此时
l,结合②③可求得此时B2=
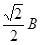 ,k=
,k=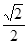 (2分)
(2分)

练习册系列答案
相关题目

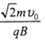 ,C点与M点的距离为
,C点与M点的距离为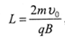 ,M点到右边界GH的垂直距离为
,M点到右边界GH的垂直距离为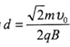 。求:
。求: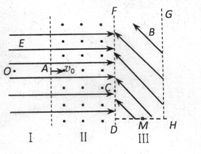
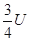 时,x轴上开始出现荧光。(不计电子的重力)试求:
时,x轴上开始出现荧光。(不计电子的重力)试求: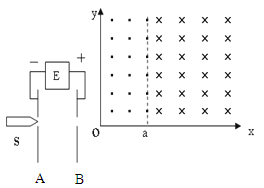
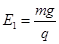 ,第四象限内电场强度大小为
,第四象限内电场强度大小为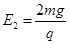 ;另有一个质量为m,带电量为q(q>0)的小球B从第二象限内的某点由静止释放,当它的运动方向变为水平方向时恰与A相撞,碰撞过程系统损失了
;另有一个质量为m,带电量为q(q>0)的小球B从第二象限内的某点由静止释放,当它的运动方向变为水平方向时恰与A相撞,碰撞过程系统损失了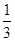 的能量,B球电荷量不变。碰后A获得沿x轴正向的速度,最后停止在P点;B球反弹后最后也打在P点。求:
的能量,B球电荷量不变。碰后A获得沿x轴正向的速度,最后停止在P点;B球反弹后最后也打在P点。求: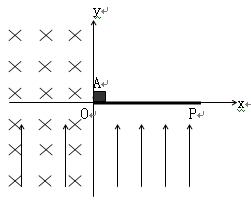
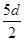 的直线,磁场方向垂直纸面向外.一质量为m、带电量为+q的粒子从y轴上P点以初速度v0垂直y轴射入匀强电场,在电场力作用下从X轴上Q点以与X轴正方向45°角进入匀强磁场.已知OQ=d,不计粒子重力.求:
的直线,磁场方向垂直纸面向外.一质量为m、带电量为+q的粒子从y轴上P点以初速度v0垂直y轴射入匀强电场,在电场力作用下从X轴上Q点以与X轴正方向45°角进入匀强磁场.已知OQ=d,不计粒子重力.求:
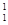 H)和二价氦离子(
H)和二价氦离子(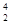 He)的混合体,经同一加速电场后,垂直射入同一偏转电场中,偏转后打在同一荧光屏上,则它们( )
He)的混合体,经同一加速电场后,垂直射入同一偏转电场中,偏转后打在同一荧光屏上,则它们( )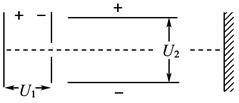


 的区域内有方向垂直坐标平面的匀强磁场.一质量为m、电荷量为q的正粒子(不计重力),从P(
的区域内有方向垂直坐标平面的匀强磁场.一质量为m、电荷量为q的正粒子(不计重力),从P(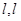 )点由静止开始运动, 通过第二象限后经
)点由静止开始运动, 通过第二象限后经 点再进入y≤0区域,并恰好经过坐标原点O.求
点再进入y≤0区域,并恰好经过坐标原点O.求
 .
.