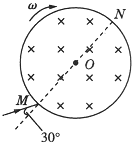
题目内容
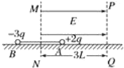
【题目】如图所示，在光滑绝缘水平面上，用长为2L的绝缘轻杆连接两个质量均为m的带电小球A和B.A球的带电量为＋2q，B球的带电量为－3q，两球组成一带电系统．虚线MN与PQ平行且相距3L，开始时A和B分别静止于虚线MN的两侧，虚线MN恰为AB两球连线的垂直平分线．若视小球为质点，不计轻杆的质量，在虚线MN、PQ间加上水平向右的电场强度为E的匀强电场后，系统开始运动．试求：
（1）B球刚进入电场时，带电系统的速度大小；
（2）带电系统向右运动的最大距离和此过程中B球电势能的变化量．
【答案】（1）
（2）
L 4qEL
【解析】
（1）设B球刚进入电场时带电系统的速度为v1，由动能定理得
2qEL＝
×2mv12
解得：
v1＝
（2）带电系统向右运动分为三段：B球进入电场前、带电系统在电场中、A球出电场后．
设A球出电场后移动的最大位移为x，对于全过程，由动能定理得
2qEL－qEL－3qEx＝0
解得
x＝
则B球移动的总位移为
xB＝L
B球从刚进入电场到带电系统向右运动到最大距离时的位移为
L
其电势能的变化量为
ΔEp＝－W＝3qE·L＝4qEL
练习册系列答案
相关题目
