题目内容
如图所示，一直角斜面体固定在地面上，右边斜面倾角60°，左边斜面倾角30°，A、B两物体分别系于一根跨过定滑轮的轻绳两端，分别置于斜面上，两物体可以看成质点，且位于同高度处于静止平衡状态，一切摩擦不计，绳子均与斜面平行，若剪断绳，让两物体从静止开始沿斜面下滑，下列叙述正确的是（ ）分析：分别对物体受力分析，由共点力的平衡即可得出两物体的质量之比；
剪断细线后，两物体在重力的作用下自由下落，由机械能守恒可求得落地的速度，由功率公式可求得两物体所受重力做功的功率之比．
剪断细线后，两物体在重力的作用下自由下落，由机械能守恒可求得落地的速度，由功率公式可求得两物体所受重力做功的功率之比．
解答：解：A、两物体位于相同高度，剪断轻绳，让两物体从静止开始沿斜面滑下，两物体运动过程中只有重力做功，
落地高度相同，根据机械能守恒定律，得mgh=
mv2
得v=
，所以到达斜面底端时两物体速率相等．故A正确．
B、取地面为参考平面可知，物体的机械能表达式为E=mgh，h相同，由于m不等，故落地时两物体机械能不等．故B错误．
C、两物体原来均处于平衡状态，受力分析得：
绳子对A、B的拉力大小相等，
对A有：mAg=Tsin60°；
对B有：mBg=Tsin30°
则有：
=
，两物体在斜面底端时速度在竖直方向上的分量之比：
=
=
，
落地时两物体重力功率的表达式为P=mgv竖，所以斜面底端时两物体重力的功率相等．故C正确．
D、两物体从静止开始沿斜面滑下做匀加速运动，根据牛顿第二定律得a=gsinθ，
根据几何关系知道A物体的加速度较大，但是下滑的距离较小，所以由公式x=
at2得知，A沿斜面下滑的时间较小，故D错误，
故选AC．
落地高度相同，根据机械能守恒定律，得mgh=
| 1 |
| 2 |
得v=
| 2gh |
B、取地面为参考平面可知，物体的机械能表达式为E=mgh，h相同，由于m不等，故落地时两物体机械能不等．故B错误．
C、两物体原来均处于平衡状态，受力分析得：
绳子对A、B的拉力大小相等，
对A有：mAg=Tsin60°；
对B有：mBg=Tsin30°
则有：
| mA |
| mB |
| 1 | ||
|
| vyA |
| vyB |
| vsin60° |
| vsin30° |
| ||
| 1 |
落地时两物体重力功率的表达式为P=mgv竖，所以斜面底端时两物体重力的功率相等．故C正确．
D、两物体从静止开始沿斜面滑下做匀加速运动，根据牛顿第二定律得a=gsinθ，
根据几何关系知道A物体的加速度较大，但是下滑的距离较小，所以由公式x=
| 1 |
| 2 |
故选AC．
点评：本题中要注意两点：（1）绳子各点处的拉力大小相等；（2）重力的功率等于重力与竖直分速度的乘积．
练习册系列答案
相关题目
如图所示，一直角斜面体放在粗糙地面上，斜面倾角分别为30°和60°，a、b两物体分别系于一根跨过定滑轮的轻绳两端，置于斜面上，a、b可看成质点，且位于同一水平高度保持静止状态，不计物体与斜面、绳与滑轮之间的摩擦，绳子与斜面平行，若剪断绳子，让a、b由静止下滑，斜面体始终静止，则（ ）
（2013?河南模拟）如图所示，一直角斜面体固定在地面上，斜面倾角分别为30°和60°，a、b两物体分别系于一根跨过定滑轮的轻绳两端，置于斜面上．a、b可看成质点，且位于同一水平高度处于静止状态，不计一切摩擦，绳子与斜面平行．若剪断绳子，让a、b由静止下滑，选水平地面为零势能参考平面（ ）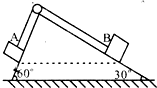
如图所示，一直角斜面体固定在水平地面上，左侧斜面倾角为60°，右侧斜面倾角为30°，A、B两个物体分别系于一根跨过定滑轮的轻绳两端且分别置于斜面上，两物体下边缘位于同一高度且处于平衡状态，不考虑所有的摩擦，滑轮两边的轻绳都平行于斜面．若剪断轻绳，让物体从静止开始沿斜面滑下，下列叙述错误的是（ ）
（2011?太原模拟）如图所示，一直角斜面固定在水平地面上，右边斜面倾角为60°，左边斜面倾角为30°，A、B两物体分别系于一根跨过定滑轮的轻绳两端，置于两斜面上，且位于同高度处于静止状态．将两物体看成质点，不计一切摩擦和滑轮质量，剪断轻绳，让两物体从静止开始沿斜面滑下，下列判断正确的是（ ）