题目内容
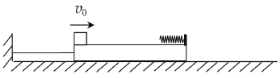
【题目】如图所示，长木板放在光滑水平面上，左端用细线系在竖直墙壁上，右侧安装有固定着轻弹簧的挡板，某时刻让一个可视为质点的滑块以速度v0从长木板左侧滑上长木板，当弹簧压缩到最短时剪断细线，最终滑块刚好回到长木板左侧. 长木板（含挡板）的质量为M，通过测量发现滑块在全过程中的位移大小为x0，滑块与木板之间的动摩擦因数为
，已知重力加速度为g，求滑块的质量m和弹簧弹性势能的最大值。
【答案】
，
【解析】
设从开始运动到弹簧最短滑块运动的距离为
，弹簧弹性势能最大为
，滑块的质量为
，
、
为细线剪断后滑块和长木板的对地位移。剪断细线后滑块和长木板组成的系统动量守恒，在任意时刻：
所以全过程：
由几何关系得：
，
从开始运动到弹簧最短由能量守恒得：
运动的全过程中能量守恒：
联立解得：
，
练习册系列答案
相关题目
