Question

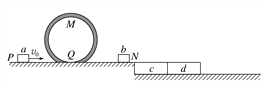
【题目】如图所示为过山车简易模型，它由光滑水平轨道和竖直面内的光滑圆形轨道组成，Q点为圆形轨道最低点，M点为最高点，圆形轨道半径R＝0.32 m.水平轨道PN右侧的水平地面上，并排放置两块长木板c、d，两木板间相互接触但不粘连，长木板上表面与水平轨道PN平齐，木板c质量m3＝2.2 kg，长L＝4 m，木板d质量m4＝4.4 kg.质量m2＝3.3 kg的小滑块b放置在轨道QN上，另一质量m1＝1.3 kg的小滑块a从P点以水平速度v0向右运动，沿圆形轨道运动一周后进入水平轨道与小滑块b发生碰撞，碰撞时间极短且碰撞过程中无机械能损失.碰后a沿原路返回到M点时，对轨道压力恰好为0.已知小滑块b与两块长木板间动摩擦因数均为μ0＝0.16，重力加速度g＝10 m/s2.

(1)求小滑块a与小滑块b碰撞后，a和b的速度大小v1和v2；

(2)若碰后滑块b在木板c、d上滑动时，木板c、d均静止不动，c、d与地面间的动摩擦因数μ至少多大？(木板c、d与地面间的动摩擦因数相同，最大静摩擦力等于滑动摩擦力)

(3)若不计木板c、d与地面间的摩擦，碰后滑块b最终恰好没有离开木板d，求滑块b在木板c上滑行的时间及木板d的长度.

Answer 1

【答案】（1） ， （2） （3） ，

【解析】(1)根据题意可知：小滑块a碰后返回到M点时：

小滑块a碰后返回到M点过程中机械能守恒： 代入数据，解得：v1＝4 m/s

取水平向右为正方向，小滑块a、b碰撞前后： 动量守恒：m1v0＝－m1v1＋m2v2

机械能守恒： 代入数据，解得：v0＝9.2 m/s，v2＝5.2 m/s

(2)若b在d上滑动时d能静止，则b在c上滑动时c和d一定能静止

解得

(3)小滑块b滑上长木板c时的加速度大小：

此时两块长木板的加速度大小：

令小滑块b在长木板c上的滑行时间为t，则：时间t内小滑块b的位移

两块长木板的位移 且x1－x2＝L

解得：t1＝1 s或 (舍去)

b刚离开长木板c时b的速度

b刚离开长木板c时d的速度

d的长度至少为x：

由动量守恒可知：

解得：v＝2 m/s

解得：x＝1.4 m