题目内容
（16分）如图所示，光滑绝缘的细圆管弯成半径为R的半圆形，固定在竖直平面内，管口B、C的连线是水平直径．现有一带正电的小球(可视为质点)从B点正上方的A点自由下落，A、B两点间距离为4R．从小球进入管口开始，整个空间中突然加上一个匀强电场，电场力在竖直向上的分力大小与重力大小相等，结果小球从管口C处脱离圆管后，其运动轨迹经过A点．设小球运动过程中带电量没有改变，重力加速度为g，求：
(1)小球到达B点的速度大小；
(2)小球受到的电场力的大小；
(3)小球经过管口C处时对圆管壁的压力．
（1）
（2）
（3）3mg 水平向右
解析试题分析：(1)小球由A自由下落到管口B的过程中机械能守恒，故有：
（2分）
（2分）
（2）设电场力的竖直分力为Fy，水平分力为Fx，则Fy=mg(方向竖直向上)
小球从B运动到C的过程中，由动能定理得：
（2分）
小球从管口C运动到A点做类平抛运动，有
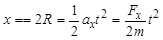（1分）
（1分）
解得：Fx=mg （1分）
电场力的大小：
（1分）
（3）小球经过管口C处时，
（1分）
设弹力N的方向向左，则：
（2分）
解得：N=3mg(方向向左) （1分）
根据牛顿第三定律可知，小球经过管口C处时对圆管的压力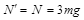
，方向水平向右 （2分）
考点：本题考查牛顿运动定律、圆周运动、平抛运动及动能定理
电子台秤放置于水平桌面上，一质量为M的框架放在台秤上，框架内有一轻弹簧上端固定在框架顶部，下端系一个质量为m的物体，物体下方用竖直细线与框架下部固定，各物体都处于静止状态。今剪断细线，物体开始振动，且框架始终没有离开台秤，弹簧不超出弹性限度，空气阻力忽略不计，重力加速度为g。则下列说法正确的是
| A．当台秤示数最小时弹簧一定处于原长位置 |
| B．当台秤示数最小时物体一定处在平衡位置 |
| C．振动过程中台秤的最大示数一定大于（M + m）g |
| D．振动过程中台秤的最大示数一定等于（M + m）g |
；现在第三象限中从P点以初速度
沿x轴方向发射质量为
，带
的离子，离子经电场后恰从坐标原点O射入磁场。
，试求P点的横坐标x；
，质量不同的带负电的粒子，经过电场加速后进入一速度选择器，从
点进入一等腰直角三角形的有界磁场中，又从斜边射出.速度选择器中垂直纸面向里的匀强磁场的磁感应强度为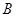
，竖直向下的匀强电场强度为
，有界磁场的磁感应强度为
，直角边长为
，
两点相距为
.求：
。A点射出的粒子从电场中运动到边界PQ时，两粒子刚好相遇.若粒子质量为m，电荷量为+q，重力不计，求：
