题目内容
空间存在着以x=0平面为分界面的两个匀强磁场,左右两边磁场的磁感应强度分别为B1和B2,且B1:B2=4:3,方向如图所示。现在原点O处一静止的中性原子,突然分裂成两个带电粒子a和b,已知a带正电荷,分裂时初速度方向为沿x轴正方向,若a粒子在第四次经过y轴时,恰好与b粒子第一次相遇。求:
小题1:a粒子在磁场B1中作圆周运动的半径与b粒子在磁场B2中圆周运动的半径之比。
|
小题1:
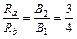
小题2:
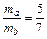
小题1: (1)原子为中性,分裂后一定有qa=-qb(b一定带负电) (2分)
原子分裂前后动量守恒,则pa+pb="0" (2分)
粒子在磁场中运动时由牛顿定律有
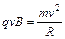 (2分)
(2分)∴
 (2分)
(2分)则:
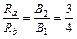 (2分)
(2分)小题2:a、b粒子相遇时:ta=tb (2分)
由题意分析可知,a粒子在第四次经过y轴与b粒子第一次相遇时,b粒子应第三次经过y轴。则
ta=Ta1+Ta2 tb=Tb1+Tb2/2 (2分)
∵
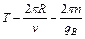 (2分)
(2分)∴
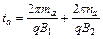

即
 (2分)
(2分)代入数据并化简得:
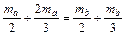
解之得:
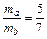

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目


 进入竖直向上的匀强电场中,如图甲所示。今测得小球进入电场后在竖直方向下降的高度y与水平方向的位移x之间的关系如图乙所示。根据图乙给出的信息,(重力加速度为g)求:
进入竖直向上的匀强电场中,如图甲所示。今测得小球进入电场后在竖直方向下降的高度y与水平方向的位移x之间的关系如图乙所示。根据图乙给出的信息,(重力加速度为g)求:
 ,间距为d,电压为u2的偏转区域,距偏转区域右侧为
,间距为d,电压为u2的偏转区域,距偏转区域右侧为 的位置是荧光屏,电子轰击荧光屏能够显示出光斑。依据上述信息,求:
的位置是荧光屏,电子轰击荧光屏能够显示出光斑。依据上述信息,求:
 kg,电荷量
kg,电荷量 ,以
,以 m/s的速度紧靠A板向上射入电场中,不计电子的重力.问电子能否射出电场?若能,计算在电场中的偏转距离;若不能,在保持电压不变的情况下,B板至少平移多少,电子才能射出电场?
m/s的速度紧靠A板向上射入电场中,不计电子的重力.问电子能否射出电场?若能,计算在电场中的偏转距离;若不能,在保持电压不变的情况下,B板至少平移多少,电子才能射出电场?
 ,自A处进入电场强度为E、方向水平向右的匀强电场,它受到的电场力恰与重力大小相等。当粒子到达图中B处时,速度大小仍为
,自A处进入电场强度为E、方向水平向右的匀强电场,它受到的电场力恰与重力大小相等。当粒子到达图中B处时,速度大小仍为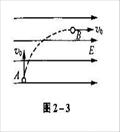


 m,间距为2.0×
m,间距为2.0× m/s的速度垂直电场方向进入电场,离开电场时偏离入射方向为5.0×
m/s的速度垂直电场方向进入电场,离开电场时偏离入射方向为5.0× m,求电子荷质比为多少?
m,求电子荷质比为多少?