题目内容
（2013?闵行区一模）如图所示，一列简谐横波沿x轴正方向传播，实线表示t=0时刻的波形，虚线表示t=0.7s时刻的波形．则这列波的（ ）分析：波沿x轴正方向传播，传播的最短距离为3m，根据波的周期性：相隔整数倍周期的时间，波形相同，得出时间与周期关系的通项，求出周期．得到频率和波速的通项．
解答：解：A、由图知：波长为λ=4m．故A正确．
B、C、D波沿x轴正方向传播，根据波形的平移法可知，t=（n+
）T，（n=0，1，2，…），则周期T=
=
s，频率f=
=
Hz，波速v=
=
（4n+3）m/s．
则当n=1时，T=0.4s．由于n是整数，f不可能等于0.25Hz，v不可能等于5.7m/s．故B正确，CD错误．
故选AB
B、C、D波沿x轴正方向传播，根据波形的平移法可知，t=（n+
| 3 |
| 4 |
| 4t |
| 4n+3 |
| 2.8 |
| 4n+3 |
| 1 |
| T |
| 4n+3 |
| 2.8 |
| λ |
| T |
| 10 |
| 7 |
则当n=1时，T=0.4s．由于n是整数，f不可能等于0.25Hz，v不可能等于5.7m/s．故B正确，CD错误．
故选AB
点评：本题关键是抓住波的周期性，得到周期的通项，进一步求出频率和波速，再求解特殊值．
练习册系列答案
相关题目
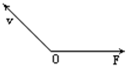（2013?闵行区一模）如图所示，一个物体在O点以初速度v开始作曲线运动，已知物体只受到恒力F作用，则物体速度大小变化情况是（ ）
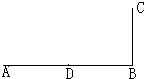（2013?闵行区一模）如图所示，有一个匀强电场，方向平行于纸面．电场中有A、B、C、D四点，已知AD=DB=BC=d，且AB⊥BC．有一个电量为q的正电荷从A点移动到B点电场力做功为2W，从B点移动到C点克服电场力做功为W．则电场中D点的电势