题目内容
20.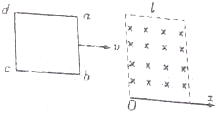 建立图中所示的x轴,边长为l、质量为m、电阻为R的正方形金属线框abcd,ab边与x轴垂直,线框以一定的初速度向右运动穿过磁场区域,运动方向始终平行于x轴,金属框的ab边进入磁场后,只考虑安培力对线框的作用,已知其速度大小与ab边的x坐标满足v=v0-kx的关系(k为已知恒量),若全属框通过磁场后恰好静止,则( )
建立图中所示的x轴,边长为l、质量为m、电阻为R的正方形金属线框abcd,ab边与x轴垂直,线框以一定的初速度向右运动穿过磁场区域,运动方向始终平行于x轴,金属框的ab边进入磁场后,只考虑安培力对线框的作用,已知其速度大小与ab边的x坐标满足v=v0-kx的关系(k为已知恒量),若全属框通过磁场后恰好静止,则( )| A. | 线框进入磁场的过程中感应电流的方向为逆时针 | |
| B. | 磁感应强度大小为$\frac{\sqrt{kmR}}{l}$ | |
| C. | 线框的初速度大小为kl | |
| D. | 线框穿过磁场的过程中产生的热量为2mk2l2 |
分析 感应电流方向根据楞次定律判断.根据F=$\frac{{B}^{2}{l}^{2}v}{R}$分析安培力与x的关系,由动能定理求磁感应强度的大小,由能量守恒定律求热量.
解答 解:A、线框进入磁场时磁通量增加,根据楞次定律知,感应电流的方向为逆时针.故A正确.
BC、根据安培力公式F=$\frac{{B}^{2}{l}^{2}v}{R}$和v=v0-kx得:
安培力大小为 F=$\frac{{B}^{2}{l}^{2}({v}_{0}-kx)}{R}$,可知,安培力随x的增大而均匀减小,线框刚进入磁场时x=0,安培力的大小为 F1=$\frac{{B}^{2}{l}^{2}{v}_{0}}{R}$.线框刚出磁场时,v=0,安培力大小为
F2=0.根据动能定理得:-$\frac{{F}_{1}+{F}_{2}}{2}$•2l=0-$\frac{1}{2}m{v}_{0}^{2}$,解得 B=$\frac{mR{v}_{0}}{2{l}^{2}}$.
由题:x=2l时,v=0,由v=v0-kx=0,得初速度为v0=2kl,代入上式得:B=$\frac{kmR}{l}$.故BC错误.
D、根据能量守恒得:产生热量为 Q=$\frac{1}{2}m{v}_{0}^{2}$=2mk2l2.故D正确.
故选:AD
点评 解决本题的关键要掌握安培力的经验公式F=$\frac{{B}^{2}{l}^{2}v}{R}$,得到F随x均匀变化,根据安培力的平均值求其做功.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列说法正确的是( )
| A. | 欧姆表的每一挡测量范围都是0到∞ | |
| B. | 欧姆表只能用来粗略地测量电阻 | |
| C. | 用欧姆表测电阻,指针越接近刻度中央,误差越大 | |
| D. | 用欧姆表测电阻,指针越接近刻度右边,误差越小 |
5.如图所示是一质点从位移原点出发的v-t图象,下列说法正确的是( )
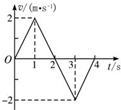

| A. | 1 s末质点离开原点最远 | B. | 2 s末质点回到原点 | ||
| C. | 3 s末质点离开原点最远 | D. | 4 s末质点回到原点 |
12.如图所示,街上的路灯由弯曲钢管支撑着处于静止状态,则钢管对路灯作用力的方向是( )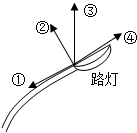

| A. | 沿钢管末端的切线方向斜向下,如图中① | |
| B. | 沿垂直钢管末端的切线方向斜向上,如图中② | |
| C. | 竖直向上,如图中③ | |
| D. | 沿钢管末端的切线方向斜向上,如图中④ |
9.关于位移和路程,下列理解正确的是( )
| A. | 位移是描述物体位置变化的物理量 | |
| B. | 路程是精确描述物体位置变化的物理量 | |
| C. | 只要运动物体的初、末位置确定,位移就确定,路程也确定 | |
| D. | 物体沿直线向某一方向运动,位移的大小等于路程 |
10.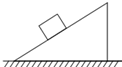 如图所示,物体和斜面都处于静止状态,对物体受力分析,哪一组是作用在物体上的按性质命名的所有力( )
如图所示,物体和斜面都处于静止状态,对物体受力分析,哪一组是作用在物体上的按性质命名的所有力( )
 如图所示,物体和斜面都处于静止状态,对物体受力分析,哪一组是作用在物体上的按性质命名的所有力( )
如图所示,物体和斜面都处于静止状态,对物体受力分析,哪一组是作用在物体上的按性质命名的所有力( )| A. | 重力、支持力、摩擦力、下滑力 | B. | 重力、压力、下滑力 | ||
| C. | 重力、支持力、摩擦力 | D. | 重力、弹力、摩擦力 |
 如图所示,质量为m的小物块从A点以初速度v0=2m/s冲上以恒定速度v=10m/s顺时针转动的传送带AB,已知传送带AB与水平夹角θ=30°,AB长20m,物块与传送带间的动摩擦因数μ=$\frac{\sqrt{3}}{2}$,问物块m是否能到达顶点B,若不能,说明理由;若能,求出到达B点时的速度大小.(g=10m/s2)
如图所示,质量为m的小物块从A点以初速度v0=2m/s冲上以恒定速度v=10m/s顺时针转动的传送带AB,已知传送带AB与水平夹角θ=30°,AB长20m,物块与传送带间的动摩擦因数μ=$\frac{\sqrt{3}}{2}$,问物块m是否能到达顶点B,若不能,说明理由;若能,求出到达B点时的速度大小.(g=10m/s2)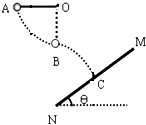 如图所示,长L=0.4m不可伸长的轻绳一端固定于O点,另一端系一质量m=0.05kg的小球,拉起小球至绳恰好伸直并处于水平后,在A点以竖直向下的初速度v0=2$\sqrt{2}$m/s释放,当小球运动至O点的正下方B点时,绳恰好断裂,小球继续运动并垂直打在同一竖直平面内且与水平面成θ=30°、无限大的挡板MN上的C点.g=10m/s2
如图所示,长L=0.4m不可伸长的轻绳一端固定于O点,另一端系一质量m=0.05kg的小球,拉起小球至绳恰好伸直并处于水平后,在A点以竖直向下的初速度v0=2$\sqrt{2}$m/s释放,当小球运动至O点的正下方B点时,绳恰好断裂,小球继续运动并垂直打在同一竖直平面内且与水平面成θ=30°、无限大的挡板MN上的C点.g=10m/s2