��Ŀ����
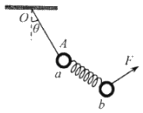
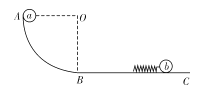
����Ŀ����ͼ��ʾ���⻬ˮƽ�����Ҷ˹̶�һ�����֣�����Ϊm����ΪL��ľ��A���������ϣ�ľ���ϱ�����벿�ֲִ��Ұ벿�ֹ⻬��������סľ��A���־�ֹ������������Ϊ![]() ����Ϊ�ʵ��ľ��B����ľ��A���Ҷˡ�һ����ϸ�߿�������֣�һ��ϵ��A���Ҷˣ���һ��ϵ����Ϊ
����Ϊ�ʵ��ľ��B����ľ��A���Ҷˡ�һ����ϸ�߿�������֣�һ��ϵ��A���Ҷˣ���һ��ϵ����Ϊ![]() �Ĺ���C������������ϸ��ˮƽ��A�������ֵľ����㹻Զ�����ɾ�ֹ��ʼ�ͷ�A����B����A�ϱ����е�ʱ��Cǡ���ŵء���֪�������ٶ�Ϊg�����ƻ��ֵ�������Ħ����
�Ĺ���C������������ϸ��ˮƽ��A�������ֵľ����㹻Զ�����ɾ�ֹ��ʼ�ͷ�A����B����A�ϱ����е�ʱ��Cǡ���ŵء���֪�������ٶ�Ϊg�����ƻ��ֵ�������Ħ����
��1������ͷ�Aʱ��ϸ�ߵ�������С��
��2�����ʱ�䣬Cǡ����ء�
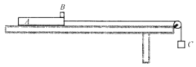
��3����Bǡ�ܻ���A����ˣ���ľ��B��A��벿�ּ�Ķ�Ħ����������
���𰸡���1��![]() ��2��2
��2��2![]() ��3��
��3��![]()
��������
(1)����A������ţ�ٵڶ����ɵã�
T��ma
����C������ţ�ٵڶ����ɵã�
![]()
��ã�
![]() ��
��![]()
(2)C���ʱAǡ���˶���![]() ������λ��ʱ�乫ʽ�ã�
������λ��ʱ�乫ʽ�ã�
![]()
��ã�
![]()
(3)B���٣�A���٣����ٶ���ͬʱǡ��B����A������ˡ�A�ij��ٶ�
![]()
A�ļ��ٶ�
aA��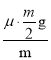 ��
��![]()
B�ļ��ٶ�
aB��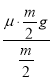 ����g
����g
�辭��ʱ��t0ʱA��B�ٶ���ͬ����
vA��aAt0��aBt0
Bǡ�ܻ���A����ˣ�λ�ƹ�ϵ��
![]()
��ã�
![]()

��ϰ��ϵ�д�
 ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д� ���������ν�ϵ�д�
���������ν�ϵ�д�
�����Ŀ