题目内容
(1)如图所示是某同学做“研究匀变速直线运动”实验时获得的一条纸带.打点计时器电源频率为50Hz.A、B、C、D、E、F、G是纸带上7个连续的点,F点由于不清晰而未画出.F点的速度v=

(2)如图甲,半径不大的圆形纸片固定在电动机转轴上,在电动机的带动下匀速转动.在圆形纸片的旁边竖直安装一个打点计时器,纸片上留下的一段痕迹如图乙所示.用这个装置可以测量电动机转动的角速度.
①在纸片转动不到一周的过程中,得到了n个清晰而且连续的点,已知打点计时器电源频率为f,要得到角速度ω的测量值,还需直接测量的物理是
②角速度ω=
(用已知的物理量和直接测量的物理量的符号表示);
③为了避免在纸片连续转动的过程中打点出现重叠,在保持电火花计时器与盘面良好接触的同时,缓慢地将电火化计时器沿圆形纸片半径方向向纸片中心移动.则纸片上打下的点的分布曲线就不是一个圆,这样做对测量结果
0.70
0.70
m/s,加速a=5
5
m/s2.
(2)如图甲,半径不大的圆形纸片固定在电动机转轴上,在电动机的带动下匀速转动.在圆形纸片的旁边竖直安装一个打点计时器,纸片上留下的一段痕迹如图乙所示.用这个装置可以测量电动机转动的角速度.
①在纸片转动不到一周的过程中,得到了n个清晰而且连续的点,已知打点计时器电源频率为f,要得到角速度ω的测量值,还需直接测量的物理是
n个点对应的圆心角θ
n个点对应的圆心角θ
(用必要的文字和字母表示);②角速度ω=
| fθ |
| n-1 |
| fθ |
| n-1 |
③为了避免在纸片连续转动的过程中打点出现重叠,在保持电火花计时器与盘面良好接触的同时,缓慢地将电火化计时器沿圆形纸片半径方向向纸片中心移动.则纸片上打下的点的分布曲线就不是一个圆,这样做对测量结果
没有
没有
(填“有”、“没有”或“无法确定”)影响.分析:(1)带实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度;
(2)①要测量转动的角度;
②角速度ω=
,测出角度,时间可以通过打点的间隔读出;
③缓慢地将电火花计时器沿圆形卡纸半径方向向卡纸中心移动.则卡纸上打下的点的分布曲线不是一个圆,而是类似一种螺旋线,点跟点间的角度没变,对测量无影响.
(2)①要测量转动的角度;
②角速度ω=
| △θ |
| △t |
③缓慢地将电火花计时器沿圆形卡纸半径方向向卡纸中心移动.则卡纸上打下的点的分布曲线不是一个圆,而是类似一种螺旋线,点跟点间的角度没变,对测量无影响.
解答:解:(1)F点瞬时速度等于EG段的平均速度,故:
vF=
=70cm/s=0.70m/s;
由图得到AB、BC、CD、DE、…距离分别为0.5cm、0.7cm、0.9cm、1.1cm、…;
根据公式△x=aT2,加速度为:a=
=
=5m/s2;
(2)①要测量转动的角度,即n个点对应的圆心角θ;
②根据ω=
,则ω=
=
,θ是n个点对应的圆心角,f是电火花计时器的打点频率.
③由于点跟点之间的角度没变化,则对测量角速度不影响.
答:(1)0.70,5;
(2)①n个点对应的圆心角θ;②
;③没有.
vF=
| 6.5cm-3.7cm |
| 0.02s×2 |
由图得到AB、BC、CD、DE、…距离分别为0.5cm、0.7cm、0.9cm、1.1cm、…;
根据公式△x=aT2,加速度为:a=
| △x |
| T2 |
| 0.2cm |
| (0.02s)2 |
(2)①要测量转动的角度,即n个点对应的圆心角θ;
②根据ω=
| △θ |
| △t |
| θ |
| (n-1)t |
| fθ |
| n-1 |
③由于点跟点之间的角度没变化,则对测量角速度不影响.
答:(1)0.70,5;
(2)①n个点对应的圆心角θ;②
| fθ |
| n-1 |
点评:本题第二问关键要知道实验的实验原理,能够根据公式ω=
列式求解,明确误差来源.
| △θ |
| △t |

练习册系列答案
相关题目



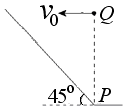
 如图所示是倾角为45°的斜坡,在斜坡底端P点正上方某一位置Q处以速度v0水平向左抛出一个小球A,小球恰好能垂直落在斜坡上,运动时间为t1.小球B从同一点Q处自由下落,下落至P点的时间为t2.不计空气阻力,则t1:t2=( )
如图所示是倾角为45°的斜坡,在斜坡底端P点正上方某一位置Q处以速度v0水平向左抛出一个小球A,小球恰好能垂直落在斜坡上,运动时间为t1.小球B从同一点Q处自由下落,下落至P点的时间为t2.不计空气阻力,则t1:t2=( ) 水平向左抛出一个小球A,小球恰好能垂直落在斜坡上,运动时间为
水平向左抛出一个小球A,小球恰好能垂直落在斜坡上,运动时间为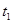 .小球B从同一点Q处自由下落,下落至P点的时间为
.小球B从同一点Q处自由下落,下落至P点的时间为 .不计空气阻力,则
.不计空气阻力,则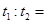 ( )
( )
 C.1∶3 D.
C.1∶3 D.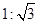


 ,
, ,光在真空中的速度为c。求:
,光在真空中的速度为c。求:
 图像,t=0时刻,小张在小王前方s0处。下列判断正确的是
图像,t=0时刻,小张在小王前方s0处。下列判断正确的是