��Ŀ����
����Ŀ����ͼ������ֱƽ���ڣ�һ�뾶ΪR�Ĺ⻬Բ�����ABC�ʹֲ�ˮƽ���PA��A�����С�BCΪԲ�������ֱ����OΪԲ�ģ�OA��OB֮��ļн���=37��һ����Ϊm��С����ԭ����ֹ��ˮƽ�����P�㣬��һˮƽ���ҵĺ���һֱ�����ڻ����ϣ�ʹ����ʼ�����˶���Ȼ��A�����Բ������˶��������������У����龭��B��ʱ��Բ�������ѹ���ﵽ�����ǡ�����˶���C�㣬��֪������ˮƽ�����Ķ�Ħ��������=0.25���������ٶ�Ϊg��sin37=0.6��cos37=0.8����
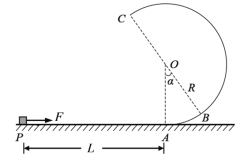
��1��ˮƽ����F�Ĵ�С�ͻ��鵽��C��ʱ�ٶ�vC�Ĵ�С��
��2��P�㵽A��ľ���L��
���𰸡�(1)0.75mg��![]() (2)
(2) ![]()
��������
���龭��B��ʱ��Բ�������ѹ���ﵽ����������ĺϳ���ˮƽ����F�Ĵ�С��ǡ�����˶���C�㣬�����ĺϳ����ָ��Բ�ĵĺ���������ţ�ٵڶ����ɿɵû��鵽��C��ʱ�ٶ�vC�Ĵ�С����P���˶���C�㣬�ɶ��ܶ����ɵ�P�㵽A��ľ�����
�⣺(1)���龭��B��ʱ��Բ�������ѹ���ﵽ��ɵ���![]()
ǡ�����˶���C�㣬�����ĺϳ����У�![]()
��ţ�ٵڶ����ɿɵã�![]()
����� ![]()
(2)��P���˶���C�㣬�ɶ��ܶ������ɵ���![]()
���![]()

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ