题目内容
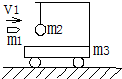 如图,一小车静止在光滑水平地面上,车顶用长L=0.8m的细线悬挂一静止小球,小车质量m3=4.0kg,小球质量m2=0.9kg,一质量为m1=0.1kg的子弹以速度v1=10m/s水平射入球内(作用时间极短,g取10m/s2),求
如图,一小车静止在光滑水平地面上,车顶用长L=0.8m的细线悬挂一静止小球,小车质量m3=4.0kg,小球质量m2=0.9kg,一质量为m1=0.1kg的子弹以速度v1=10m/s水平射入球内(作用时间极短,g取10m/s2),求(1)细线上摆的最大角度θ.
(2)小球第一次返回最低点时,小球的速度和小车的速度.
分析:(1)本题子弹射入小球的过程、共同体向上摆动的过程和向下摆动三个过程研究:弹射入小球的过程遵守动量守恒,即可求出子弹与球作用后的共同速度;共同体向上摆动的过程,到最高点时,子弹、球与小车三者达到共同速度,根据系统水平方向动量守恒求出此时的共同速度,再对系统运用机械能守恒定律求出最大角度θ.
(2)小球第一次返回最低点时,根据整个过程水平方向动量守恒和机械能守恒列方程,即可求解此时两者的速度.
(2)小球第一次返回最低点时,根据整个过程水平方向动量守恒和机械能守恒列方程,即可求解此时两者的速度.
解答:解:(1)子弹与球作用后,子弹与球共同速度v2,
子弹与球动量守恒:m1v1=(m1+m2)v2
解得:v2=1.0m/s
子弹与球摆到最高点时,子弹、球与小车三者达到共同速度v3,
子弹、球与小车动量守恒:m1v1=(m1+m2+m3)v3
解得:v3=0.2m/s
子弹与球作用后到子弹与球摆到最高点,子弹、球与小车三者机械能守恒:
(m1+m2)v22-
(m1+m2+m3)v32=(m1+m2)gh
得:h=
=0.
根据数学知识得,cosθ=
=
则得,θ=60°.
(2)设小球第一次返回最低点时,小球和小车的速度分别为v4、v5,
子弹与球作用后,水平方向动量守恒:
(m1+m2)v2=(m1+m2)v4+m3v5
子弹、球与小车三者机械能守恒:
(m1+m2)v22=
(m1+m2)v42+
m3v52
得:v4=
v2=-0.6m/s,方向向左.
v5=
v2=0.4m/s,方向向右.
答:
(1)细线上摆的最大角度θ为60°.
(2)小球第一次返回最低点时,小球的速度为-0.6m/s,小车的速度为0.4m/s.
子弹与球动量守恒:m1v1=(m1+m2)v2
解得:v2=1.0m/s
子弹与球摆到最高点时,子弹、球与小车三者达到共同速度v3,
子弹、球与小车动量守恒:m1v1=(m1+m2+m3)v3
解得:v3=0.2m/s
子弹与球作用后到子弹与球摆到最高点,子弹、球与小车三者机械能守恒:
| 1 |
| 2 |
| 1 |
| 2 |
得:h=
| m12m3v12 |
| 2(m1+m2)2(m1+m2+m3)g |
根据数学知识得,cosθ=
| L-h |
| L |
| 1 |
| 2 |
则得,θ=60°.
(2)设小球第一次返回最低点时,小球和小车的速度分别为v4、v5,
子弹与球作用后,水平方向动量守恒:
(m1+m2)v2=(m1+m2)v4+m3v5
子弹、球与小车三者机械能守恒:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
得:v4=
| (m1+m2)-m3 |
| (m1+m2+m3) |
v5=
| 2(m1+m2) |
| (m1+m2+m3) |
答:
(1)细线上摆的最大角度θ为60°.
(2)小球第一次返回最低点时,小球的速度为-0.6m/s,小车的速度为0.4m/s.
点评:分析物体经历的过程,把握每个所遵守的物理规律是应具有基本能力.本题要注意系统只是水平方向动量守恒,而总动量并不守恒.

练习册系列答案
相关题目
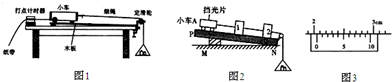
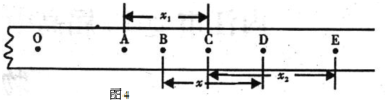
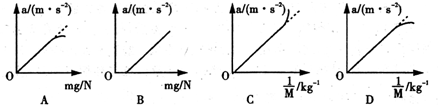
 某同学在“研究小车的加速度与质量关系“的探究实验中,使用的装置如图所示.他将光电门固定在光滑水平轨道上的某点B,用同一重物拉不同质量的小车,每次小车都从同一位置A由静止释放.
某同学在“研究小车的加速度与质量关系“的探究实验中,使用的装置如图所示.他将光电门固定在光滑水平轨道上的某点B,用同一重物拉不同质量的小车,每次小车都从同一位置A由静止释放.
 .
.

