题目内容
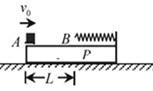
【题目】如图所示,木板P静置于光滑水平面上,质量为m,P的右端固定一轻质弹簧,左端A与弹簧的自由端B相距L。质量为2m且可以看作质点的物块以速度v0从A点滑上木板,物块压缩弹簧后被弹回并停在A点(弹簧始终在弹性限度内)。物块与P之间的动摩擦因数为μ,求:
(1)求P的最终速度v1;
(2)求此过程中弹簧最大压缩量x;
(3)求此过程中弹簧的最大弹性势能Ep。
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]()
【解析】
(1)因水平面光滑,物块和木板组成的系统动量守恒,则有
![]()
代入数值可求得![]() 。
。
(2)当滑块和木板第一次共速时,二者距离最小,弹簧压缩量最大
从最初到最后匀速整个过程由功能关系可知系统减少动能等于生成内能
![]()
解得![]() 。
。
(3)当滑块和木板第一次共速时,二者距离最小,弹簧压缩量最大,弹性势能最大
由动量守恒可得第一共速和第二次共速时速度都是![]()
由能量守恒关系可知
![]()
联立解得![]() 。
。

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目