题目内容
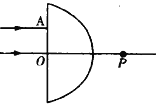
【题目】如图所示，半球形玻璃的球半径为R，一束平行的激光束垂直射到半球形玻璃的左侧面上，其中一条光线沿直线穿过玻璃，它的入射点是O；另一条光线的入射点为A，穿过玻璃后两条光线交于P点，OA＝
，OP＝
R。若在半球形玻璃的左侧面上贴上不透光的纸片，激光束不从曲面上直接透射出去，则该纸片的最小面积为多大?
【答案】
【解析】作出光路图如图所示．
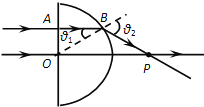
一条光线沿直线进入玻璃，在半圆面上的入射点为B，入射角设为θ1，折射角设为θ2，则： 
，
得
因OP=
R，由几何关系知 BP=R，则折射角
θ2=2θ1=60°
由折射定律得玻璃的折射率为
n=
=
=．
若光线恰在曲面上发生全反射，则 sinC=
根据几何知识可知，此时从曲面上直接射出去的光线在圆面上是以O为圆心、半径为r的圆．
则 sinC=
因而该纸片的最小面积为 S=πr2
联立解得 S=
答：该纸片的最小面积为．
练习册系列答案
相关题目
