题目内容
用细线系一小球在竖直平面内做圆周运动,已知小球在最高点的速度是4m/s,最低点的速度是6m/s,小球通过圆周最低点和最高点时,绳上张力之差为30N,细线长为
0.5
0.5
m小球的质量为0.5
0.5
kg.(不计一切阻力,取g=10m/s2)分析:对物体在最高点和最低点分别受力分析,找出向心力来源,根据牛顿第二定律和向心力公式列式求解!
解答:解:球经过最高点时,受重力和绳子的拉力,如图
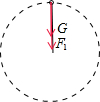
根据牛顿第二定律得到,F1+mg=m
球经过最低点时,受重力和绳子的拉力,如图
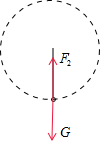
根据牛顿第二定律得到,F2-mg=m
由题意得到,F2-F1=30N;
联立以上三式可解得:m=0.5kg;l=0.5m
故答案为:0.5m 0.5kg

根据牛顿第二定律得到,F1+mg=m
| v12 |
| l |
球经过最低点时,受重力和绳子的拉力,如图

根据牛顿第二定律得到,F2-mg=m
| v22 |
| l |
由题意得到,F2-F1=30N;
联立以上三式可解得:m=0.5kg;l=0.5m
故答案为:0.5m 0.5kg
点评:本题关键对物体在最高点和最低点分别受力分析,找出向心力来源,然后根据牛顿第二定律列式求解!题目中并没有说明空气阻力忽略不计,不可用机械能守恒定律!

练习册系列答案
相关题目