题目内容
9. 如图所示,有一透明介质球,球心为O,半径为R,光线DC平行于直线AOB射到介质球上的C点,DC与AB的距离H=$\frac{\sqrt{3}}{2}$R.若DC光线进入介质球后,经一次反射再次回到介质球的界面时,从球内折射出的光线与入射光线平行,求介质的折射率.
如图所示,有一透明介质球,球心为O,半径为R,光线DC平行于直线AOB射到介质球上的C点,DC与AB的距离H=$\frac{\sqrt{3}}{2}$R.若DC光线进入介质球后,经一次反射再次回到介质球的界面时,从球内折射出的光线与入射光线平行,求介质的折射率.
分析 由题光线经两次折射、一次反射后与入射光线平行,则光路具有对称性,作出光路图.根据几何知识求出第一次折射时的入射角i和折射角r,由折射定律求出折射率.
解答 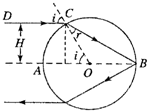 解:设光线在C点折射时入射角为i,折射角为r,
解:设光线在C点折射时入射角为i,折射角为r,
由几何知识可得
sini=$\frac{H}{R}$=$\frac{\sqrt{3}}{2}$
解得 i=60°
光在球内发生反射,根据对称性作出光路图如图.
由2r=i,得到r=30°
故介质的折射率 n=$\frac{sini}{sinr}$=$\sqrt{3}$
答:介质的折射率为$\sqrt{3}$.
点评 本题的关键在于根据对称性,作出光路图.还要抓住光线在球形玻璃砖内传播时,第一次折射时折射角等于等于第二次折射时的入射角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.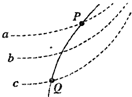 如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
 如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )| A. | 三个等势面中,a的电势最高 | |
| B. | 带电质点在P点具有的电势能比在Q点具有的电势能大 | |
| C. | 带电质点通过P点时的动能比通过Q点时大 | |
| D. | 带电质点通过P点时的加速度比通过Q点时大 |
14.我国“神州七号”飞船成功地将三名宇航员送入太空并安全返回.如果把“神州七号”载人飞船绕地球运行看作是同一轨道上的匀速圆周运动,宇航员测得自己绕地心做匀速圆周运动周期为T,且已知地球半径为R,地球表面重力加速度为g,万有引力恒量为G.根据以上数据不可确定的物理量有( )
| A. | 地球的质量 | B. | 飞船线速度的大小 | ||
| C. | 飞船所需的向心力 | D. | 飞船离地面的高度 |
19. 长直导线与矩形线框abcd处在同一平面中静止不动,如图甲所示.长直导线中通以大小和方向都随时间做周期性变化的电流,i-t图象如图乙所示.规定沿长直导线方向上的电流为正方向.关于最初一个周期内矩形线框中感应电流的方向,下列说法正确的是( )
长直导线与矩形线框abcd处在同一平面中静止不动,如图甲所示.长直导线中通以大小和方向都随时间做周期性变化的电流,i-t图象如图乙所示.规定沿长直导线方向上的电流为正方向.关于最初一个周期内矩形线框中感应电流的方向,下列说法正确的是( )
 长直导线与矩形线框abcd处在同一平面中静止不动,如图甲所示.长直导线中通以大小和方向都随时间做周期性变化的电流,i-t图象如图乙所示.规定沿长直导线方向上的电流为正方向.关于最初一个周期内矩形线框中感应电流的方向,下列说法正确的是( )
长直导线与矩形线框abcd处在同一平面中静止不动,如图甲所示.长直导线中通以大小和方向都随时间做周期性变化的电流,i-t图象如图乙所示.规定沿长直导线方向上的电流为正方向.关于最初一个周期内矩形线框中感应电流的方向,下列说法正确的是( )| A. | 由顺时针方向变为逆时针方向 | |
| B. | 由逆时针方向变为顺时针方向 | |
| C. | 由顺时针方向变为逆时针方向,再变为顺时针方向 | |
| D. | 由逆时针方向变为顺时针方向,再变为逆时针方向 |
 如图所示,行星A和B绕恒星C做匀速圆周运动,圆半径之比为4:1,某一时刻A,B,C在一条直线上,B经过时间t绕恒星C运动一周,则要使A,B,C重新在一条直线(B在A,C中间)上,至少要经过的时间是$\frac{8}{7}t$.
如图所示,行星A和B绕恒星C做匀速圆周运动,圆半径之比为4:1,某一时刻A,B,C在一条直线上,B经过时间t绕恒星C运动一周,则要使A,B,C重新在一条直线(B在A,C中间)上,至少要经过的时间是$\frac{8}{7}t$.

 某同学为探究“恒力做功与物体动能改变的关系”,设计了如下实验,他的操作步骤是:
某同学为探究“恒力做功与物体动能改变的关系”,设计了如下实验,他的操作步骤是: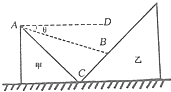 如图所示,一小物块从斜面甲的上部A点自静止下滑,又滑上另一斜面,到达B点的速度为零.已知两斜面倾角不同,但小物块与两斜面的动摩擦因数相同,若AB连线与水平线AD的夹角为θ,求小物块与斜面间的动摩擦因数(不计小物块在C处碰撞中的能量损失).
如图所示,一小物块从斜面甲的上部A点自静止下滑,又滑上另一斜面,到达B点的速度为零.已知两斜面倾角不同,但小物块与两斜面的动摩擦因数相同,若AB连线与水平线AD的夹角为θ,求小物块与斜面间的动摩擦因数(不计小物块在C处碰撞中的能量损失).