Question

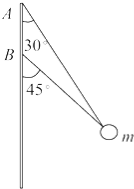
【题目】（12分）（2015春石家庄校级期中）如图所示，两绳系一质量为0.1kg的小球，两绳的另一端分别固定于轴的A、B两处，上面绳长2m，两绳拉直时与轴的夹角分别为30°和45°，问球的角速度在什么范围内两绳始终有张力？（g取10m/s2）

Answer 1

【答案】球的角速度在rad/s＜ω＜rad/s 时，两绳始终有张力．

【解析】

试题分析：当上绳绷紧，下绳恰好伸直但无张力时，由上绳子的拉力和重力的合力提供向心力，根据牛顿第二定律列式求解出最小角速度；

当下绳绷紧，上绳恰好伸直但无张力时，由下绳子的拉力和重力的合力提供向心力，根据牛顿第二定律列式求解出最大角速度；即可求得角速度的范围．

解：当上绳绷紧，下绳恰好伸直但无张力时，小球受力如下图

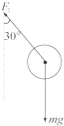
由牛顿第二定律得：mgtan30°=mω12r；

又有：r=Lsin30°

解得：ω1=rad/s；

当下绳绷紧，上绳恰好伸直无张力时，小球受力如下图

由牛顿第二定律得：mgtan45°=mω22r；

解得：ω2=rad/s；

故当 rad/s＜ω＜rad/s 时，两绳始终有张力．

答：球的角速度在rad/s＜ω＜rad/s 时，两绳始终有张力．