题目内容
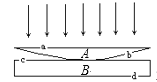
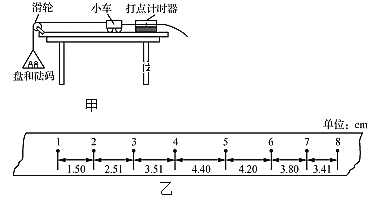
【题目】在光滑的水平面上有一质量M=2kg的木板A,其上表面Q处的左侧粗糙,右侧光滑,且PQ间距离L=2m,如图所示;木板A右端挡板上固定一根轻质弹簧,在靠近木板左端的P处有一大小忽略不计质量m=2kg的滑块B.某时刻木板A以vA=1m/s的速度向左滑行,同时滑块B以vB=5m/s的速度向右滑行,当滑块B与P处相距3L/4时,二者刚好处于相对静止状态.若在二者共同运动方向的前方有一障碍物,木板A与它相碰后仍以原速率反弹(碰后立即描去该障碍物),求:

(1)B与A的粗糙面之间的动摩擦因数μ;
(2)滑块B最终停在木板A上的位置. (g取10m/s2).
【答案】(1)0.6;(2)0.17m
【解析】
试题①木板A与障碍物发生碰撞前、后两个过程中,木板和滑块系统,由动量守恒定律和能量守恒定律列出等式求解
(1)设M、m共同速度为v,定水平向右为正方向,
由动量守恒定律得mvB-MvA=(M+m)v①
解得:v=2m/s
对A、B组成的系统,由能量守恒![]() MvA2+
MvA2+![]() mvB2
mvB2![]() (M+m)v2=μmg
(M+m)v2=μmg![]() L③
L③
代入数据得μ=0.6
(2)木板A与障碍物发生碰撞后以原速率反弹,假设B向右滑行并与弹簧发生相互作用,
当A、B再次处于相对静止状态时,两者的共同速度为u,在此过程中,A、B和弹簧组成的系统动量守恒、能量守恒.
由动量守恒定律得mv-Mv=(M+m)u④
u=0
设B相对A的路程为S,由能量守恒得![]() (M+m)v2=μmgs⑤
(M+m)v2=μmgs⑤
代入数据得s=![]() m
m
由于s>![]() L,所以B滑过Q点并与弹簧相互作用,然后相对A向左滑动到Q点左边,
L,所以B滑过Q点并与弹簧相互作用,然后相对A向左滑动到Q点左边,
设离Q点距离为s1
.s1=s![]() L=0.17m
L=0.17m

练习册系列答案
相关题目