��Ŀ����
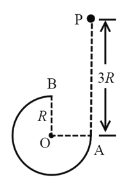
����Ŀ����ͼ��ʾ���뾶R=0.5m�Ĺ⻬Բ����CDM�ֱ���⻬б����ABC��б��MN������C��M�㣬OΪԲ��Բ�ģ�DΪԲ����͵㣮б����ABC�̶��ڵ����ϣ�����B��װһ�����֣�һ������ϸ����������֣����ƻ���Ħ�����ֱ�����С���P��Q������ϸ���ֱ����Ӧб��ƽ�У���������P��Q����龲ֹ����PC���ΪL1=0.25m��б��MN�㹻�������Q����m=4kg����MN��Ķ�Ħ��������=![]() ����sin
����sin![]() =0.6��cos
=0.6��cos![]() =0.8��
=0.8��
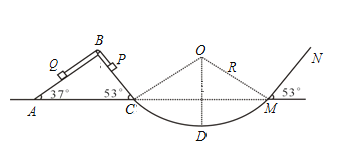
��1���ն�ϸ�������P��һ�ε���D��ʱ�Թ����ѹ����С��
��2�����P��һ�ι�M���0.3s����K�㣬��MK�����
��3�����P��MNб���ϻ��е���·�̣�
���𰸡���1��78N��2��0.17m��3��1.0m
��������
(1)������P��D���̣��ɶ��ܶ������ã�
mgh=![]()
���ݼ��ι�ϵ���У�
h=L1![]() +R��1��
+R��1��![]() ��
��
��D�㣬֧�����������ĺ����ṩ�����������У�
FD��mg=![]()
�������ݽ�ã�
FD=78N
��ţ�ٵ������ɵã����P�Թ����ѹ����СΪ78N��
(2)PM�Σ����ݶ��ܶ������У�
m1gL1![]() =
=![]()
�������ݽ�ã�
vM=2m/s
��MN�����˶����̣�����ţ�ٵڶ����ɣ��õ���
a1=g![]() +��g
+��g![]() =10m/s2
=10m/s2
�����ٶ�ʱ�乫ʽ���У�
vM=a1t1
�������ݽ�ã�
t1=0.2s
����t1=0.2sʱ��P�ﵽ��б��MN����ߵ㣬�ʷ��ع��̣��У�
![]()
��MN�����˶����̣�����ţ�ٵڶ����ɣ��У�
a2=g![]() ����g
����g![]() =6m/s2
=6m/s2
�ʣ������˶�ѧ��ʽ���У�
xMK=![]()
��MK֮��ľ���Ϊ0.17m��
(3)���������CM֮�����ػ������ҵ���M��ʱ�ٶ�Ϊ�㣬�Դ�P��M�������ö��ܶ������õ���
mgL1![]() ����mgL1
����mgL1![]() L��=0
L��=0
�������ݽ�ã�
L��=1.0m
�����P��MNб���ϻ��е���·��Ϊ1.0m��