题目内容
16. 有a、b、c、d四颗地球卫星,a还未发射,在赤道表面上随地球一起转动,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,它们均做匀速圆周运动,各卫星排列位置如图所示,则( )
有a、b、c、d四颗地球卫星,a还未发射,在赤道表面上随地球一起转动,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,它们均做匀速圆周运动,各卫星排列位置如图所示,则( )| A. | 在相同时间内a转过的弧长最长 | |
| B. | b的向心加速度近似等于重力加速度g | |
| C. | c在6h内转过的圆心角是$\frac{π}{2}$ | |
| D. | d的运动周期有可能是22h |
分析 近地轨道卫星的向心加速度约为g.根据万有引力提供向心力,列出等式得出角速度与半径的关系,分析弧长关系.根据开普勒第三定律判断d与c的周期关系.
解答 解:A、由$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$,得v=$\sqrt{\frac{GM}{r}}$,卫星的半径越大,线速度越小,所以b的线速度比c、d大,而a与C的角速度相等,根据v=ωr可知,a的线速度小于c的线速度,则在相同时间内b转过的弧长最长.故A错误;
B、b是近地轨道卫星,则其向心加速度约为g.故B正确;
C、c是地球同步卫星,周期是24h,则c在6h内转过的圆心角是$\frac{π}{2}$.故C正确;
D、由开普勒第三定律$\frac{{R}^{3}}{{T}^{2}}$=k知,卫星的半径越大,周期越大,所以d的运动周期大于c的周期24h.故D错误;
故选:BC.
点评 对于卫星问题,要建立物理模型,根据万有引力提供向心力,分析各量之间的关系,并且要知道同步卫星的条件和特点.

练习册系列答案
相关题目
7.在“探究求合力的方法”实验中,现有木板、白纸、图钉、橡皮筋、细绳套和一把弹簧秤.
(1)为完成实验,某同学另找来一根弹簧,先测量其劲度系数得到的实验数据如表:
根据表中数据在图甲中作出F-x图象并求得该弹簧的劲度系数k=54N/m;(结果保留两位有效数字)
(2)某次实验中,弹簧秤的指针位置如图乙所示,其读数为2.10N

(3)实验对两次拉伸橡皮条的要求中,下列哪些说法是正确的BD(填字母代号).
A.将橡皮条拉伸相同长度即可
B.将橡皮条沿相同方向拉到相同长度
C.将弹簧秤都拉伸到相同刻度
D.将橡皮条和绳的结点拉到相同位置
(4)同学们在操作过程中有如下议论,其中对减小实验误差有益的说法是B(填字母代号).
A.两细绳必须等长
B.弹簧秤、细绳、橡皮条都应与木板平行
C.用两弹簧同时拉细绳时两细绳必须垂直以便计算出合力
D.拉橡皮条的细绳要长些,标记同一细绳方向的两点要近些.
(1)为完成实验,某同学另找来一根弹簧,先测量其劲度系数得到的实验数据如表:
| 弹力F(N) | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 |
| 伸长量x(×10-2 m) | 0.74 | 1.80 | 2.80 | 3.72 | 4.60 | 5.58 | 6.42 |
(2)某次实验中,弹簧秤的指针位置如图乙所示,其读数为2.10N

(3)实验对两次拉伸橡皮条的要求中,下列哪些说法是正确的BD(填字母代号).
A.将橡皮条拉伸相同长度即可
B.将橡皮条沿相同方向拉到相同长度
C.将弹簧秤都拉伸到相同刻度
D.将橡皮条和绳的结点拉到相同位置
(4)同学们在操作过程中有如下议论,其中对减小实验误差有益的说法是B(填字母代号).
A.两细绳必须等长
B.弹簧秤、细绳、橡皮条都应与木板平行
C.用两弹簧同时拉细绳时两细绳必须垂直以便计算出合力
D.拉橡皮条的细绳要长些,标记同一细绳方向的两点要近些.
4.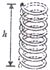 一根长为l的硬质直管弯制成如图所示的竖直放置的等螺距,螺线管(外形类似于弹簧,但是由管道弯制而成),螺线管高为h,管道内径很小,一直径略小于管道内径的光滑小球从上端管口由静止释放,重力加速度为g,关于小球的运动,下列说法正确的是( )
一根长为l的硬质直管弯制成如图所示的竖直放置的等螺距,螺线管(外形类似于弹簧,但是由管道弯制而成),螺线管高为h,管道内径很小,一直径略小于管道内径的光滑小球从上端管口由静止释放,重力加速度为g,关于小球的运动,下列说法正确的是( )
 一根长为l的硬质直管弯制成如图所示的竖直放置的等螺距,螺线管(外形类似于弹簧,但是由管道弯制而成),螺线管高为h,管道内径很小,一直径略小于管道内径的光滑小球从上端管口由静止释放,重力加速度为g,关于小球的运动,下列说法正确的是( )
一根长为l的硬质直管弯制成如图所示的竖直放置的等螺距,螺线管(外形类似于弹簧,但是由管道弯制而成),螺线管高为h,管道内径很小,一直径略小于管道内径的光滑小球从上端管口由静止释放,重力加速度为g,关于小球的运动,下列说法正确的是( )| A. | 小球在运动过程中受管道的作用力越来越大 | |
| B. | 小球在运动过程中受到管道的作用力始终为$\frac{mg\sqrt{{l}^{2}-{h}^{2}}}{l}$ | |
| C. | 小球到达下端管口时重力的功率为mg$\sqrt{2gh}$ | |
| D. | 小球到达下端的时间为$\sqrt{\frac{2{l}^{2}}{gh}}$ |
11.一电子飞经电场中A、B两点,电子在A点电势能为4.8×10-17 J,动能为3.2×10-17 J,电子经过B点时电势能为3.2×10-17 J,如果电子只受电场力作用,则下列说法错误的是( )
| A. | 电子在B点时动能为4.8×10-17J | B. | 由A到B电场力做功为100eV | ||
| C. | 电子在B点时动能为1.6×10-17J | D. | A、B两点间电势差为-100V |
1.下列说法正确的是 ( )
| A. | 用加温、加压或改变其化学状态的方法都不能改变原子核衰变的半衰期 | |
| B. | 放射性元素的半衰期是指大量该元素的原子核中有半数发生衰变需要的时间 | |
| C. | 中子与质子结合成氘核时吸收能量 | |
| D. | ${\;}_{7}^{14}$N+${\;}_{2}^{4}$He→${\;}_{8}^{17}$O+${\;}_{1}^{1}$H是核聚变 | |
| E. | 氪90(9036Kr)是不稳定的,经过4次β衰变最终成为稳定的锆90(9040Zr) |
8.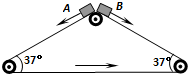 三角形传送带以2m/s的速度逆时针匀速转动,两边的传送带长都是3m且与水平方向的夹角均为37°,现有两个小物块A、B从传送带顶端都以2m/s的初速度沿传送带下滑,物块与传送带间的动摩擦因数都是0.5,已知g取10m/s2,sin37°=0.6,cos37°=0.8.下列说法正确的是( )
三角形传送带以2m/s的速度逆时针匀速转动,两边的传送带长都是3m且与水平方向的夹角均为37°,现有两个小物块A、B从传送带顶端都以2m/s的初速度沿传送带下滑,物块与传送带间的动摩擦因数都是0.5,已知g取10m/s2,sin37°=0.6,cos37°=0.8.下列说法正确的是( )
 三角形传送带以2m/s的速度逆时针匀速转动,两边的传送带长都是3m且与水平方向的夹角均为37°,现有两个小物块A、B从传送带顶端都以2m/s的初速度沿传送带下滑,物块与传送带间的动摩擦因数都是0.5,已知g取10m/s2,sin37°=0.6,cos37°=0.8.下列说法正确的是( )
三角形传送带以2m/s的速度逆时针匀速转动,两边的传送带长都是3m且与水平方向的夹角均为37°,现有两个小物块A、B从传送带顶端都以2m/s的初速度沿传送带下滑,物块与传送带间的动摩擦因数都是0.5,已知g取10m/s2,sin37°=0.6,cos37°=0.8.下列说法正确的是( )| A. | 物块A先到达传送带底端 | |
| B. | 传送带对物块A、B均做负功 | |
| C. | 物块A、B在传送带上的划痕长度之比为1:3 | |
| D. | 物块AB在传送带上的划痕之比为1:5 |
5.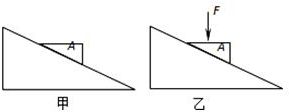 如图甲所示,斜面体静止在粗糙的水平地面上,斜面体上有一小滑块A沿斜面匀速下滑,现对小滑块施加一竖直向下的作用力F,如图乙所示两种情景下斜面体均处于静止状态,则下列说法正确的是( )
如图甲所示,斜面体静止在粗糙的水平地面上,斜面体上有一小滑块A沿斜面匀速下滑,现对小滑块施加一竖直向下的作用力F,如图乙所示两种情景下斜面体均处于静止状态,则下列说法正确的是( )
 如图甲所示,斜面体静止在粗糙的水平地面上,斜面体上有一小滑块A沿斜面匀速下滑,现对小滑块施加一竖直向下的作用力F,如图乙所示两种情景下斜面体均处于静止状态,则下列说法正确的是( )
如图甲所示,斜面体静止在粗糙的水平地面上,斜面体上有一小滑块A沿斜面匀速下滑,现对小滑块施加一竖直向下的作用力F,如图乙所示两种情景下斜面体均处于静止状态,则下列说法正确的是( )| A. | 施加力F后,小滑块A受到的滑动摩擦力增大 | |
| B. | 施加力F后,小滑块A将加速下滑 | |
| C. | 施加力F后,地面对斜面体的支持力增大 | |
| D. | 施加力F后,地面对斜面体的摩擦力增大 |