题目内容
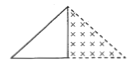
【题目】如图所示,轻弹簧一端固定在倾角为θ的光滑斜面底端,弹簧上端放着质量为m的物体A,处于静止状态.将一个质量为2m的物体B轻放在A上,则在A、B一起向下运动过程中

A.放在A上的瞬间,B对A的压力大小为![]() mgsin θ
mgsin θ
B.A、B的速度先增大后减小
C.A、B间的弹力先增大后减小
D.A、B运动到最低点时,弹簧的弹力大小为5mgsin θ
【答案】ABD
【解析】
A、在放B之前,物体A保持静止状态,重力的分力和弹簧的弹力平衡:
F=mgsinθ;
在放B瞬间,对A、B整体研究,根据牛顿第二定律有:
(2m+m)gsinθ-F=3ma
解得:
![]()
对物体B受力分析,根据牛顿第二定律有:
2mgsinθ-N=2ma:
解得:
N=![]() mgsinθ.
mgsinθ.
由牛顿第二定律知,B对A的压力大小为![]() mgsinθ.故A正确,
mgsinθ.故A正确,
B、由于在AB向下运动过程中,弹簧的弹力一直增大,3mgsinθ先大于弹力,后小于弹力,则A、B的速度先增大后减小。故B正确。
C、对AB整体,合力先减小后增大,加速度先减小后反向增大,当加速度沿斜面向下时,根据牛顿第二定律有:
2mgsinθ-N=2ma
知a减小,N增大。
当加速度沿斜面向上时,根据牛顿第二定律有:
N-2mgsinθ=2ma
知a增大,N增大,则A、B间的弹力一直增大,故C错误;
D开始时弹簧被压缩
![]()
放上物体B后的平衡位置弹簧被压缩
![]()
此过程弹簧被压缩
![]()
由对称可知,到达最低点时弹簧被压缩
![]()
即此时弹簧的弹力大小为5mgsinθ,选项D正确;
故选ABD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目