题目内容
如图所示，竖直放置的足够长平行光滑金属导轨ab、cd，处在垂直导轨平面向里的水平匀强磁场中，其上端连接一个阻值为R=0.40Ω的电阻；质量为m=0.01kg、电阻为r=0.30Ω的金属棒MN紧贴在导轨上，保持良好接触。现使金属棒MN由静止开始下滑，通过位移传感器测出下滑的位移大小与时间的关系如下表所示，导轨电阻不计，重力加速度g取l0m/s2。试求：
（1）当t=1.0s瞬间，电阻R两端电压U大小；
（2）金属棒MN在开始运动的前1s内，电阻R上产生的热量；
（3）从开始运动到t=1.0s的时间内，通过电阻R的电量。
（2）金属棒MN在开始运动的前1s内，电阻R上产生的热量；
（3）从开始运动到t=1.0s的时间内，通过电阻R的电量。
解：（1）从位移与时间关系数据可知，从0.8s以后，金属棒MN已经做匀速运动，速度大小为
vm=
m/s
又当匀速运动时，应有：
所以Bl=0.1
故在t=1.0s瞬间，电阻R两端电压U=
0.4V
（2）金属棒MN下滑1s的过程中，由动能定理
mgx－W安=
所以W安=0.158J
电阻R上产生的热量为Q=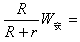
0.09J
（3）通过电阻R的电量为
vm=
m/s又当匀速运动时，应有：
所以Bl=0.1
故在t=1.0s瞬间，电阻R两端电压U=
0.4V （2）金属棒MN下滑1s的过程中，由动能定理
mgx－W安=
所以W安=0.158J
电阻R上产生的热量为Q=
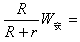0.09J （3）通过电阻R的电量为
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
如图所示，竖直放置的光滑圆环上套有一质量为m的小球，小球经过最高点时的速度为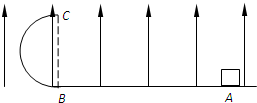
如图所示，竖直放置的半圆形绝缘轨道半径为R，下端与绝缘水平面平滑连接，整个装置处于方向竖直向上的匀强电场E中．一质量为m、带电量为+q的物块（可视为质点），从水平面上的A点以初速度v0水平向左运动，沿半圆形轨道恰好通过最高点C，场强大小
如图所示，竖直放置的轻弹簧一端固定在地面上，另一端与斜面体P固定，P与斜放的固定挡板MN接触且处于静止状态，则斜面体P此刻受到外力的个数可能是（ ）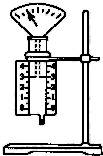
物理选修3-3
如图所示，竖直放置的U形导轨宽为L，上端串有电阻R（其余导体部分的电阻都忽略不计）．磁感应强度为B的匀强磁场方向垂直于纸面向外．金属棒ab的质量为m，与导轨接触良好，不计摩擦．从静止释放后ab保持水平而下滑．试求